Kriging Interpolation Comparison on Alberta Weather Station Elevation Data using System for Automated Geoscientific Analysis (SAGA GIS)

Kriging Interpolation Comparison on Alberta Weather Station Elevation Data using System for Automated Geoscientific Analysis (SAGA GIS)

Introduction

Purpose

The purpose of this tutorial is to provide a step-by-step guide to using the Kriging interpolation technique in SAGA GIS, a software that many users may not have encountered before. The tutorial will introduce the various types of Kriging and the key variables to consider during the process. By comparing results from a dataset with dense data points to one with sparse data, the tutorial aims to highlight the critical role that data quality and quantity play in achieving accurate interpolation results.

Introduction to SAGA

SAGA, short for System for Automated Geoscientific Analyses, is a powerful Geographic Information System (GIS) software designed for the effective implementation of spatial algorithms. It offers a comprehensive and ever-growing suite of geoscientific methods, coupled with an approachable user interface featuring diverse visualization options. SAGA runs on both Windows and Linux operating systems and is distributed as Free Open Source Software (FOSS).

Downloading SAGA

Before beginning the tutorial, if you do not have SAGA GIS please follow the steps below:

• Follow this link to download [1]
• Once the download is complete extract the files from the zip folder
• Run the saga_gui.exe to open the program

Data

Transformed Data used in tutorial is available in the Download Tutorial Data section

Acquiring the Data

To download the Elevation data follow these steps:

• Visit the Scholars GeoPortal.
• In the search bar enter Weather Stations .
• The Canadian Weather Stations should be available to Add to map.
• After adding the data to the map it is possible to select an area. In our case we selected All of Alberta's data.
• Once this is completed, go to the Download page and either download your selected area or the entire dataset.

To download the Alberta boundary file follow these steps:

• Visit the Open Canada
• Download the Provinces/Territories, Cartographic Boundary File - 2016 Census
• Clip to only Alberta or Province of choice. (Clipped Data Available In Download Tutorial Data Section)

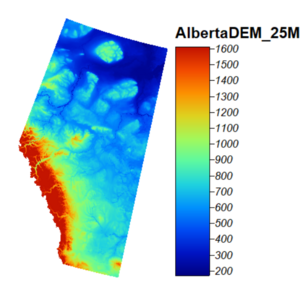
To download the Alberta 25M Digital Elevation Model follow these steps:

• Go to Altalis.com
• Create Altalis account to download the free 25M Digital Elevation Model
• Add the 25M Raster DEM to your cart.
• Go to cart and Proceed with Download.
• An email with your file ready to download will be sent to you shortly.

Download Tutorial Data

All the data and code can be downloaded from this Google Drive Link

The download contains:

TutorialDataDownload.zip (124KB)

• Alberta Boundary Shapefile (152KB)
• Alberta Weather Station Data (100KB)
• Limited Alberta Weather Station Data (30.4KB)

AlbertaDEM.zip(1.18GB) *Optional

• Alberta 25M Digital Elevation Model (8.25GB)

Tutorial

SAGA GIS Interpolation Options

Saga has four different types of interpolation, each with their own strengths and weaknesses. We will explain the use cases of each of them. They also have a 3D Kriging tool that we will not go into detail in this tutorial. There are also lots of different options and inputs that modify the kriging in SAGA which we will explain and how they impact the interpolation.

• Ordinary Kriging
  • Assumptions: Assumes the mean of the data is unknown but constant over the area of interest.
  • Advantages: Simple, widely applicable, and does not require external data or a predefined trend.
  • Use Case: Best for spatially autocorrelated data with no obvious trends or external influencing factors.
• Regression Kriging
  • Assumptions: Combines a deterministic regression model with kriging of residuals.
  • Advantages: Incorporates additional explanatory variables (e.g., slope, aspect) to improve accuracy.
  • Use Case: Ideal when auxiliary data strongly influences the spatial distribution of the variable.
• Simple Kriging
  • Assumptions: Assumes a known and constant mean across the study area.
  • Advantages: Computationally efficient and straightforward but requires prior knowledge of the mean.
  • Use Case: Rarely used unless the mean is well-established (e.g., synthetic datasets).
• Universal Kriging
  • Assumptions: Assumes the data has a deterministic trend (e.g., polynomial or linear) over space.
  • Advantages: Models and accounts for spatial trends while still relying on kriging for local variation.
  • Use Case: Useful for non-stationary data with a noticeable trend (e.g., elevation gradients across a region).

Kriging Interpolation Setup

Step 1: Open the Data Files

• Navigate to File → Open.
• Open each data file individually. (the files with .shp file format)
• Ensure all the data has been added correctly. Go to the Manager tab → Data → Tree

Figure 1: Data Successfully Imported

Step 2: Add Files to the Map

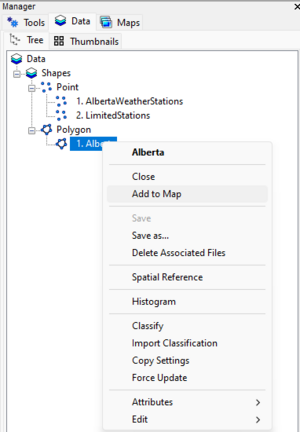
• Right-click on each file and select Add to Map.
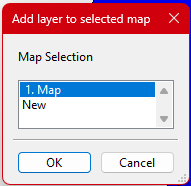
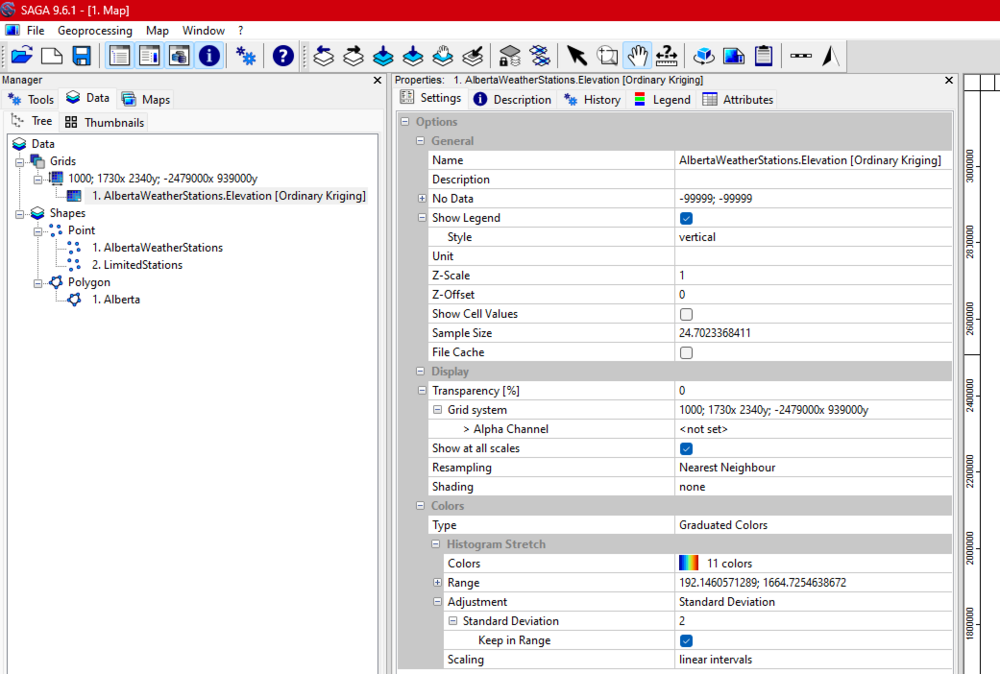
• Ensure that all files are added to the same map. Avoid creating separate maps for each file. ( See Figure 2 through 4 for the exact steps and expected outcome.)

Figure 2: Adding Files to a Map

Figure 3: Choose the Desired Map

Figure 4: Expected Outcome

Step 3: Kriging Analysis Setup

• Go to Geoprocessing tab.
• Navigate to Spatial and Geostatistics → Kriging → Ordinary Kriging. (Figure 5 demonstrates this step.)

Figure 5: Kriging Tool Path

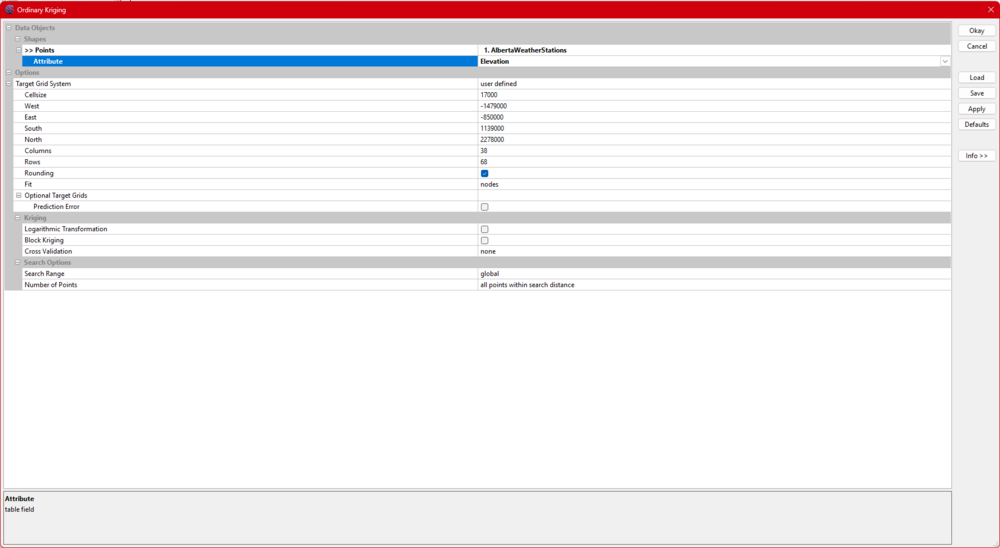
Step 4: Adjust Kriging Settings

• Use the default Kriging settings for your initial analysis. (Figure 6 shows these settings.)
• For extended boundaries, customize the settings as needed. In this case we are expanding the boundaries so the interpolated area covers all of Alberta (Refer to Figure 7 for details.)
  • Extended boundaries are a preferred option as they give a better result.

Figure 6: Default Kriging Extent

Figure 7: Expanded Extent

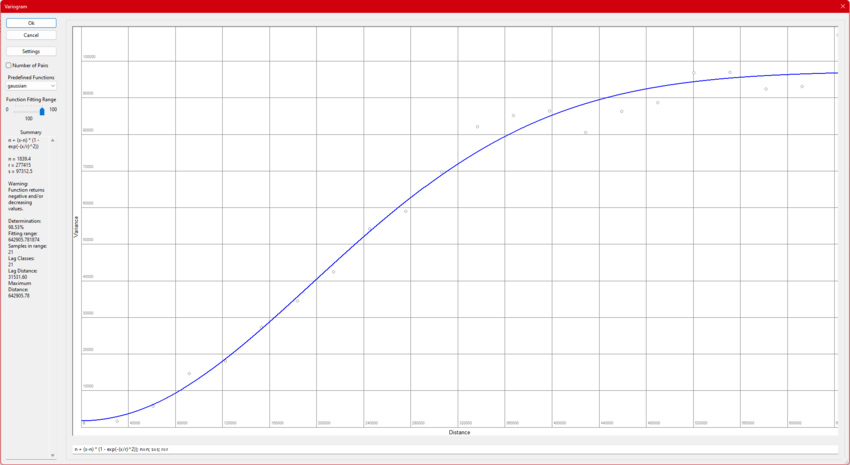
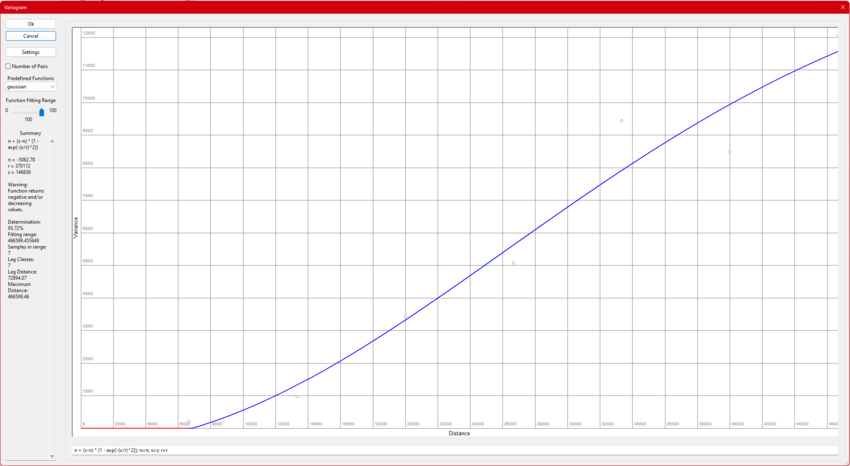
Step 5: Variogram

• Variograms help in modeling spatial patterns by describing how the variance of data values varies with distance. Because it directly affects the accuracy of Kriging predictions, choosing the variogram with the best determination (Best fit to you data) is essential. By reducing interpolation mistakes and guaranteeing that the model appropriately depicts spatial relationships, a well-fitted variograms improves the dependability of your results. Poor variogram selection can lead to biased predictions or the underestimation of variability.

• In the case of this tutorial both datasets used 100 for the Function Fitting Range.
  • This could cause issues with overfit noise or irrelevant patterns, leading to inaccurate predictions. Please take the time to find the best fitting range for your data.
• Both data models also used Gaussian Predefined Functions.
  • This function had the best fit (Determination) with the data used.

• Once this process is completed press Ok

Variogram All Weather Stations

Variogram Limited Weather Stations

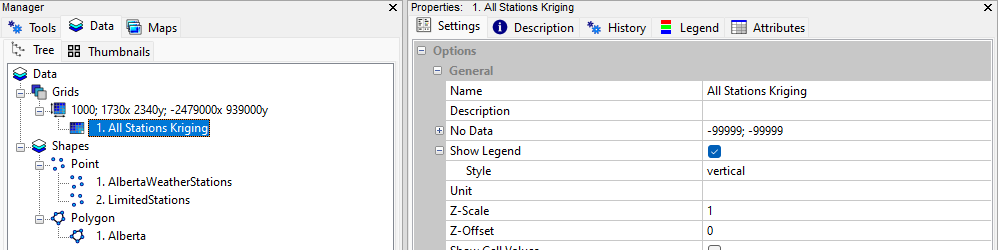
Step 6: Save Kriging Results

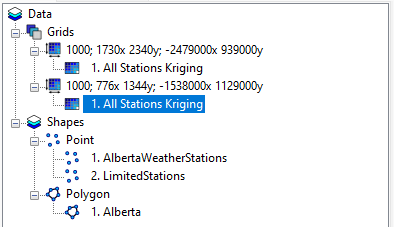
• After completing the Kriging analysis, locate the results in the Data tab under Grids.
• Rename the result to something meaningful, e.g., "Kriging Analysis".

(Figures 9 and 10 display this process.)

Figure 9: Kriging Result location

Figure 10: Kriging Result Change name

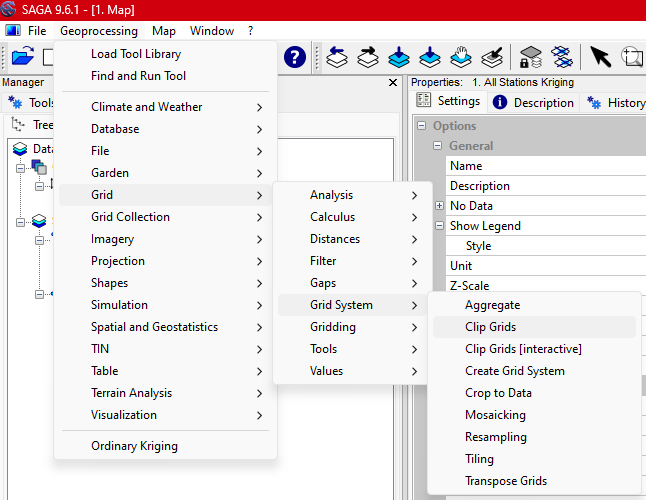
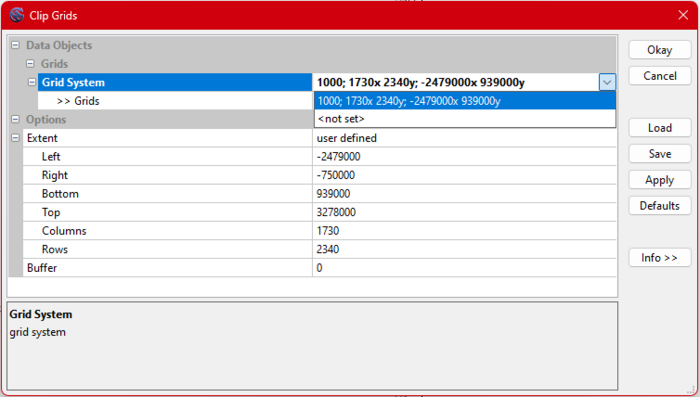
Step 7: Clip the Kriging Results

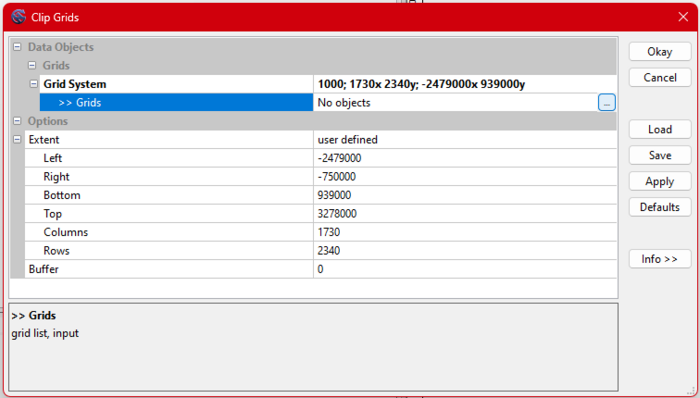
• Go to Geoprocessing → Grid → Grid System → Clip Grids. (Figure 11 shows this menu.)
• Select the appropriate grid system.
• Use the polygon selection tool to clip the data to the Alberta region:
  • Choose the dotted grid selection.
  • Use the three dots and two arrows tool to define the clip area.
  • Specify Alberta as the clipping region.

(Refer to Figures 11-15 for guidance.)

Figure 11: Path to Clip Tool

Figure 12: Selecting the Correct Grid System

Figure 13: Clicking on the 3 dots to Select a Grid

Figure 14: Moving the Correct Grid to the Right

Figure 15: Selecting the Alberta Polygon to Clip the Grid

Step 8: Rename Clipped Results

• Rename the clipped Kriging results to differentiate them from the original dataset.
• Update the map view to reflect these changes.

(Figures 16 demonstrate this step.)

Figure 16: Rename Clipped Results

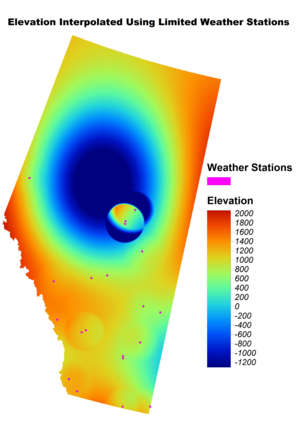
Step 9: Repeat for Limited Weather Station Data

• Repeat the Kriging analysis and clipping process, this time using data from a limited number of weather stations.
• Ensure the same steps are followed to maintain consistency.

Go back to Step 3 and repeat using limited weather stations data.

Compare Results

For Variogram analysis and visualization + interpretation.

Final All Weather stations layout

Final Limited Weather Stations Layout

Alberta Digital Elevation Model (25M) Layout

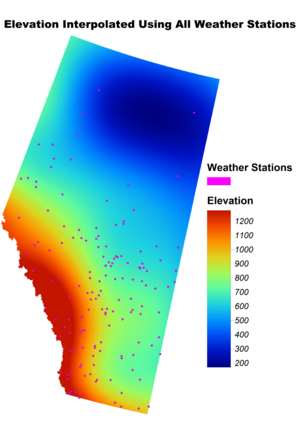
Comparing the Accuracy of the Interpolations

The Root Mean Square Error (RMSE) is a common metric used to quantify the differences between the observed and predicted values, calculated using the formula

RMSE Formula

The interpolation using all the available weather station had an RMSE of 243 compared to an RMSE of 933 with the limited points. Therefor, on average the completed points is 4x more accurate while have more than 6x the data.