Georeferencing Raster Imagery in SAGA GIS

Introduction

Geo-referencing

In the last few decades the extensive use of GPS navigation systems through the widespread use of the Internet in mobile phones, and thus the numerous multimedia applications that make use of geolocation technologies, has increased the use of maps exponentially, and with it cartographic document management (Jiménez-Pelayo; Bonachera-Cano, 2001; Beltrán-López, 2012). All these technologies and the primary uses for which they were designed have allowed us to both review and revitalise the way of presenting, disseminating and making the cartographic and photographic documentation stored and digitised in archives, libraries, map libraries, museums, geographic institutes and other institutions publicly accessible (Cascón-Katchadourian; Ruiz-Rodríguez, 2016). Alongside many other possible uses, georeferencing technologies applied to cartographic sources allow us to convert the image from the digitalisation of old maps (Crespo-Sanz; Fernández-Wyttenbach, 2011) into an interactive layer that can be displayed in a Geographic Information System (GIS) through a web browser or a mobile app (Maptiler, 2017). This is possible by assigning geographic coordinates to an element that did not have them, and embedding it in related applications of widespread universal use such as Google Maps.

Geo-location technologies applied to old photographic collections allow us to discover where the images were taken, find out what is shown in many of them and, above all, facilitate the user to search through.

Much of the data in the world can be geo-referenced, which indicates the importance of geospatial big data handling. Geospatial data describe objects and things with relation to geographic space, often with location coordinates in 3 a spatial referencing system. Geospatial data are traditionally collected using ground surveying, photogrammetry and remote sensing, and more recently through laser scanning, mobile mapping, geo-located sensors, geo-tagged web contents, volunteer geographic information (VGI), global navigation satellite system (GNSS) tracking and so on. Raster data produced by scanning aerial photographs, toposheets, or print maps normally do not contain any spatial reference information. Other times, the image does not properly align with other data, and requires transformation in order to be used in conjunction with existing data. Georeferencing rasters is a means of accomplishing both courses of action, and is a common and important task in the field of geospatial analysis (especially when working with historical imagery or maps). ESRI defines Georeferencing as:

Aligning geographic data to a known coordinate system so it can be viewed, queried, and analyzed with other geographic data. Georeferencing may involve shifting, rotating, scaling, skewing, and in some cases warping, rubber sheeting, or orthorectifying the data. citation

This tutorial contains an introduction to the process of georeferencing imagery in the SAGA GIS software, as well as information on the fundamentals of the georeferencing process.

Georeferencing options are complex; what works for architectural workflows may not be suitable for GIS workflows. Different regions of the Earth have different geographical requirements. Since the earth is not a perfect sphere, it is not a straightforward process to project a map onto the earth’s surface, or transfer an object onto the surface. Projections are mathematical formulas that translate the shape of the earth onto a 2D page. Because the translation loses data, different projections represent the longitudinal and latitudinal coordinates of the non-uniform sphere on the page. When georeferencing is enabled, each design layer stores information that describes the mapping of that layer’s Cartesian coordinate system onto a geographic coordinate system of latitude and longitude. The origin offset determines how the projection relates to the internal origin (the center of the drawing in the Vectorworks file); this offset can be turned off at the document level or at the layer level for GIS workflows. If all or most design layers will have the same georeferencing information, use the Georeferencing command to set the parameters for the document. After the default document georeferencing is set, edit each design layer to enable georeferencing, and to customize the settings for individual layers, if needed.

Geolocation:

Geolocation consists of determining the precise situation occupied by a given object in space, according to its latitude, longitude, and height coordinates

Geo-refencing definition: Georeferencing is the process of aligning the raster dataset, with the help of real-world coordinates, to its actual position on the earth (globe) (Esri, 2018). Georeferencing refers to the process of assigning map coordinates to image data. It allows to define the existence of a raster image in the physical space. Rectification is also known as geo-referencing. The alignment of an image to a map so that the image is planimetric, just like the map (Jensen, 2004). The process by which the geometry of an image is made planimetric (Jensen, 1986).

Why geo-referencing When data from different sources are combined in GIS analysis, it is required to align them properly with the help of geo-referencing. As the raster is made up of pixels, it does not store any information regarding location, so we cannot use it in real-world location until is it geo-referenced. To calculate the exact area or extent of a raster dataset. Satellite images inherent some un-systematic errors making its location shifted to the original xy-location. Georeferencing is the process of aligning the geohraphic dataset, to a known coordinate system so it can be viewed, queried, and analysed with another geographic dataset.

This example uses absolute geo-referencing (image to map rectification) of google earth, topo-sheets and grown control point.

In cartography, georeferencing processes follow the identification of homologous points in the coordinate systems of two documents of different origin: 1) the raster coordinates system of a digitised ancient map without geographic coordinates; and 2) the coordinates system of a support map or reference cartography (Dávila-Martínez; Camacho-Arranz, 2012). The process usually consists of establishing a common location which both the reference cartography and the cartography without georeferencing share with certainty, and that has been maintained over time (geographical features, monuments, streets), thus indicating to the SIG that those two points in both maps are geographically the same (Figure 1); the more control points which are created, the more accurate the georeferencing will be (Arcgis, 2013; 2016).

What does "georeferenced" mean? Georeferencing means that the internal coordinate system of a map or aerial photo image can be related to a ground system of geographic coordinates. The relevant coordinate transforms are typically stored within the image file (GeoPDF and GeoTIFF are examples), though there are many possible mechanisms for implementing georeferencing. The most visible effect of georeferencing is that display software can show ground coordinates (such as latitude/longitude or UTM coordinates) and also measure ground distances and areas.

Its use allows to revitalise and give new purpose to numerous and diverse ancient cartography that remains in archive deposits, libraries and cultural centres. Geo-referencing, with the help of digitization and web publication, facilitates access for non-expert users to geographical, heritage, urban or environmental information of interest. This technique allows us to embed the old map in current maps such Google Maps, Bing Maps or similar, and by means of transparency sensors, compare them, making possible the development of evolutionary historical studies by urbanists, historians or architects on how a city, a state or a territory has evolved.

This article evaluates the interest and scope of document management of both technologies, analyses its contemporary application in cartographic and photographic management, and offers a systematised review of a significant number of practical cases from public and private institutions that have recently implemented their documentary heritage with success.

Coordinate Systems

Locations on the earth’s surface are measured in terms of coordinates, a set of two or more numbers that specifies a location in relation to a reference system, the graticule grid. The graticule specifies positions on the globe with latitude and longitude coordinates. The graticule refers to longitude and latitude on a three-dimensional globe. The graticule is based on an east-west scale called longitude and a north-south scale called latitude. When we use longitude and latitude on a two-dimensional map, we refer to these as geographic coordinates.

Projections

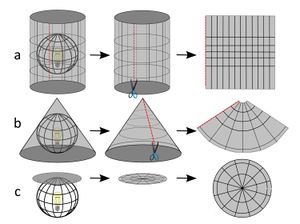
Beyond the specified uses and applications, geo-referencing is today an important area of study within the field of cartography (Witmer et al., 2006; Hill, 2009; Long et al., 2016). It is a fundamental element of ancient cartography, as it allows us to accurately reconstruct the geographical situation of plans on a large scale and without projections. The term “map projection” refers to both the process and product of transforming spatial coordinates on a three-dimensional sphere to a two-dimensional plane. In terms of actual mechanics, most projections use mathematical functions that take as inputs locations on the sphere and translate them into locations on a two-dimensional surface.

It is helpful to think about projections in physical terms. If you had a clear globe the size of a beach ball and placed a light inside this globe, it would cast shadows onto a surrounding surface. If this surface were a piece of paper that you wrapped around the globe, you could carefully trace these shadows onto the paper, then flatten out this piece of paper and have your projection!

Projection basics are as follows:

• Four properties that can be distorted include area, shape, distance and/or direction. Simply put, a map is not a perfect representation of the features on the surface of the world – the globe is far more accurate.
• Projections are designed such that one or more of these properties suffers little (no) distortion. Two important projection types are conformal and equal-area. Each of these two projection types is suited to particular uses. Conformal maintains shape and direction and is well suited to navigation. Equal-area is obviously well suited to uses where area calculations (i.e. absolute size of polygons) or density values (i.e. number of trees per hectare) are important.
• Projections can be envisioned as a large piece of ‘photographic’ paper wrapped around a globe. A light inside the globe is turned on and features on the surface of the globe are projected onto the photographic paper. The photographic paper generally takes 3 shapes: cylinder, cone or just left flat. These three shapes are known as developable surfaces because they can be (unwrapped) laid flat without tearing or distortion – as compared to ‘peeling’ the skin off the globe and trying to lay it flat on a table with tearing. Cylindrical and conic projections are most common. A cylinder will touch (be tangent) along the equator and is thus best suited to equatorial regions of the world. A cone will rest on the globe at mid-latitude. Thus it is well suited to countries in the mid latitudes and especially those with a wide east-west dimension (i.e. Canada, China).
• Deciding which projection is best requires that you consider:
  • Which property is to be preserved
  • Location (primarily latitiude) of the area of interest

Figure 3: Planar, conical, and cylindrical projections

Datum

Datum is a reference surface used to generate coordinates (i.e. latitude and longitude). Latitudes and longitude are angular measures, given in degrees. Although latitudes/longitudes are really determined from the surface of the earth, it is easier to imagine yourself in the centre of the world looking out at the earth’s surface.

Imagine looking out at the equator. You would be looking straight out (i.e. flat), therefore your angle would be zero – indeed this is the latitude of the equator. Now imagine looking at VIU (in B.C. Canada). You would be looking up at an angle of about 49 degrees (latitude) from the equator. Looking straight up at Santa’s workshop equates to a right angle, or 90 degrees.

For longitude you start by looking out at Greenwich, England. That is your zero degree mark. As you turn towards the Atlantic Ocean you are turning west. Central America has longitudes around 90 degrees west. Note that 90 degrees East Longitude would run through Asia. So Longitudes go off in both directions from Greenwich and meet in the Pacific at 180 degrees (the international dateline). If the world was perfectly round we could stop here. Unfortunately …

… the world is not a perfect sphere. It’s more of an ellipsoid. This is because the earth is not a hardened rock (centre is molten, also surface is about 75% water). Since the earth spins, centrifugal force pulls out the earth at the equator. But wait, it gets uglier yet. The surface of the earth, and therefore the shape of the earth, is essentially mean sea level (m.s.l.). M.S.L. is determined not only by centrifugal force (pushing out at the equator) but also by earth’s gravity (that force that makes apples fall down instead of up). Here’s the kicker … m.s.l. is not a smooth, perfect ellipsoid. It is essentially a dented ellipsoid (more properly known as a geoid). This is because gravity is not constant. Mass and density of an object determine gravity. The density and mass of the earth’s crust varies, · therefore, gravity varies, · therefore, m.s.l. varies, · therefore, the earth’s surface is an ellipsoid with slight undulations.

It is easy to determine the latitudes and longitudes (a.k.a. the graticule) for a sphere. Figuring out the graticule on an ellipsoid is a manageable task. But determining the graticule on the irregular geoid is very complicated. In the end it was decided that for small-scale maps a sphere would do just fine, but for medium and large-scale maps (1:250,000 to 1:5,000) an ellipse would be more accurate. (The math for the geoid is just too complicated to bother with).

The only complications are: 1. An ellipse that best approximates North America is not the best ellipse for Europe. Thus each part of the world uses its own ellipse. The ellipse used and how it is anchored to the earth is what is known as datum. 2. Our understanding of the earth’s true shape continues to change as technology changes – thus new datums continue to be developed.

For example, the datum (i.e. ellipse) used for North America in 1927 was based on an ellipse developed in 1866. This was known as NAD27 (for North America Datum 1927). After satellites were deployed and better measures of the earth were acquired, a new ellipse was developed in 1980. In 1983 it was decided to use this new ellipse for mapping in North America. The new datum is known as NAD83. Belize City did not move between 1927 and 1983. However, Belize City has different latitude and longitude under NAD83 than it did under NAD27. Indeed, some places in North America had a difference equivalent to 300 metres.

Datums have ‘nothing to do with’ distortions – they have ‘everything to do with’ location … specifically the coordinate (lat/long) of a feature on the earth’s surface. Datum is the choice of ellipsoid to use. As the graticule (latitude/longitude) varies from ellipsoid to ellipsoid, changing datums will change the coordinates of a feature on the earth’s surface. Therefore, when features from different maps are combined onto one map (i.e. for an analysis in GIS) it is essential that the maps be of the same datum.

SAGA GIS

Figure 1: SAGA GIS Logo

For the following tutorial, System for Automated Geoscientific Analyses, or SAGA GIS software will be used. SAGA GIS is a free, open-source geographic information system program, originally developed by a small team of researchers from the Department of Physical Geography in the University of Gottingen, Germany.When the SAGA GIS team began development in 2001, the purpose of the software was aligned with the needs of the development team, such as the analysis of raster imagery, with a focus on digital elevation models (DEM). SAGA has also been designed for an easy and effective implementation of spatial algorithms. Over the years, however, the software has broadened in scope, as it has seen many feature contributions from its world-wide user community. Interestingly, the users have freedom of improving the program, modifying it and releasing the improvements to the public. This resulted in a comprehensive, growing set of geo-scientific methods combined an easily approachable user interface with many visualization options. The software is available for Windows, Linux, and FreeBSD operating systems. (http://www.saga-gis.org/en/index.html)

Features

• Object oriented system design (C++)
• Modular structure allows framework independent function development
• SAGA API with immense support for geodata handling
• GUI for intuitive data management, analysis and visualization
• Runs on Linux as well as on Windows operating systems
• Portable software running without installation even from memory sticks (MSW)
• Free and Open Source Software (FOSS)
• Scripting via command line, Python, Java, R
• Far more than 450 freely available functions for geodata analysis
• Georeferencing and cartographic projections
• Grid interpolation of scattered point data, triangulation, IDW, splines, ...
• Vector tools: clipping, buffer zones, raster to vector conversion, ...
• Image analysis: filters, supervised classification, PCA, FFT, OBIA, ...
• Geostatistics: GWR, variograms, ordinary & universal Kriging, ...
• Terrain analysis: morphometry, hydrology, illumination, classification, ...
• and many more ...

Figure 2: Capablities of SAGA GIS

Installation Instructions

The latest version of SAGA GIS can be downloaded on the SAGA GIS Sourceforge page. At the time of writing, the latest version of SAGA GIS is 6.4.0. Documentation for the SAGA GIS tool library can be found in the SAGA-GIS Tool Library Documentation

Data Acquisition

For the following tutorials, you will need to acquire imagery from two sources: Satelite imagery from Google Earth, and a PDF toposheet or scanned print map.

Google Earth

For this tutorial, we will be using imagery from google earth. to obtain this imagery, perform the following steps.

1. ensure that you have downloaded and installed Google Earth on your computer
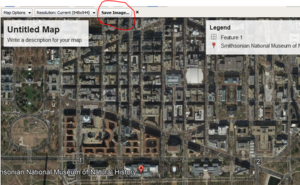
2. Open Google Earth, and zoom to the area of interest of your choice. for this tutorial, we used the area around the Smithsonian Museum of Natural History in Washington, DC, USA, but any location will suffice.
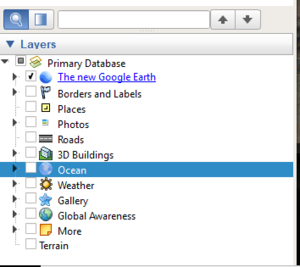
3. In the Layers menu in the bottom left corner of your screen, uncheck all layers. Google earth renders terrain in 3d, and the perspective this creates can distort your exported imagery (See Figure 2).
   
   
   

   Figure 2: Layers Menu of Google Earth
   
   
   
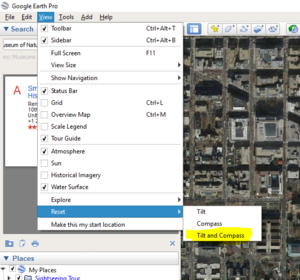
4. Ensure that your imagery is north-facing and vertically-angled by selecting View -> Reset -> Tilt and Compass in the menu bar at the top of the screen (See Figure 3)
   
   
   

   Figure 3: Resetting the Angle and Rotation of Google Earth
   
   
   
5. Under Tools -> Options, ensure that under Show Lat/Long, Universal Transverse Mercator is selected.
6. Using the Add Placemark tool (See Figure 4), add four or more placemarks to your screen. make note of their coordinates and label them numerically. change their icon to one that is more precise, location-wise.
   
   
   

   Figure 4: Adding Placemarks in Google Earth
   
   
   
7. Save your image by selecting File -> Save -> Save Image in the menu bar at the top of the screen. then, press the Save Image Button (See Figure 5).
   
   
   

   Figure 5: Saving Your Image
   
   
   

Print Map

For this tutorial, we will be using a scan of a historical watershed boundary map of Alberta, made available through the Open Government License. the following pre-tutorial steps must be performed:

1. Download the file from the following link. you can use any other PDF or raster map as long as it contains some sort of absolute location information.
2. If necessary, convert the pdf to a raster TIF file. many free websites exist to perform this conversion, such as PDFaid.com. Ensure that the conversion is performed at a high enough DPI that all text is legible. for this tutorial, we chose 150 DPI.
3. Save the converted file in a working directory of your choice.

Tutorial

Georeferencing a Historical Map

In the following tutorial, the process of georeferencing a historical map in SAGA GIS will be explained. To begin, we will import the image into SAGA GIS.

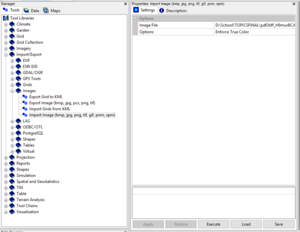
1. In the Tools tab, select Import/Export -> Images -> Import Image
2. In the Image File field, select the historical map you downloaded earlier
3. In the Options field. select Enforce True Colour
4. Double click your imported file in the Data Tab in order to view the file.
   
   
   

   Figure 6: Importing Imagery into SAGA GIS
   
   
   

Creating Ground Control Points

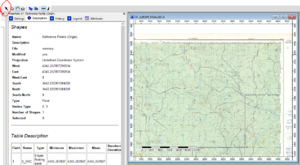
In order to georeference an image, we use Ground Control Points (GCPs). these are points that establish a relationship between the pixel coordinate system of the raster to a coordinate system of the earth. GCPs are typically placed at sharp features such as intersections or easily visible landmarks, but for this map, we will use sections of the map graticule with known coordinates.

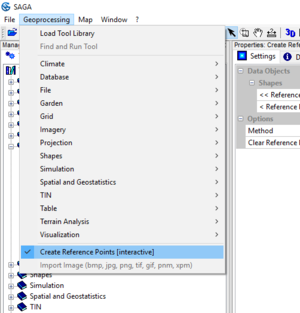
1. To start creating the GCPs, we will run the Create Reference Points module. in the Tools tab, select Projection -> Georeferencing -> Create Reference Points [Interactive]'.
2. Click the Okay button in the pop-up menu. this module creates a shapefile with two attribute fields, used to store the latitude and longitude of a point.
3. Zoom to an area of the imported file with known coordinates, such as the intersection of two known graticules (See figure 7).
   
   
   

   Figure 7: Initial GCP Location
   
   
   
4. Select the Action button (See figure 8), and click the location of your first GCP. in the pop-up window, enter the x and y (on earth) coordinates of that point.
   
   
   

   Figure 8: Action Button
   
   
   
5. Repeat this process at least four more times, each with a different point. Once you have completed this, end the module by selecting Geoprocessing -> Create Reference Points [Interactive] in the menu bar at the top of the screen (See figure 9).
   
   
   

   Figure 9: Ending a Module
   
   
   

Defining Projection

We must now add projection information to the image. According to our map, the projection used is NAD 1927 UTM.

1. Open the Set Coordinate Reference System module. in the Tools tab, select Projection -> Proj.4 -> Set Coordinate Reference System. Select the User Defined field, and in the popup menu, change the Projection Type field to Universal Transverse Mercator (UTM). in the Predefined Datum Field, select North_American_Datum_1927. In the popup menu, press Okay. (See Figure 10
   
   
   

   Figure 10: Setting a Coordinate System
   
   
   
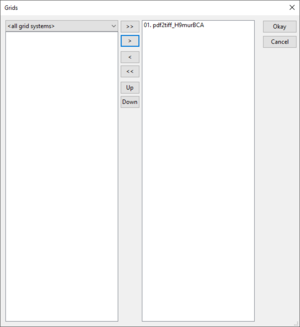
2. In the module menu, under the Data Objects section, select the Grids Field. A popup menu will open up. Select your image file and click the > button to transfer it to the right side of the popup menu. Click Okay to finish. (see Figure 11)
   
   
   

   Figure 11: Selecting a grid in the Data Objects Menu
   
   
   

Georeferencing the Grid

We now possess all the necessary components to Georeference the map.

1. Open the Rectify Grid module. in the Tools tab, select Projection -> Georeferencing -> Rectify Grid.
2. In the Reference Points (origin) Field, select your generated GCP shapefile. in the Grid System Field, select the grid system of your imported map. In the Grid field, select your imported image (make sure it is the one that you defined a projection for). In the Method field, select Automatic (these choices will be explained in the following tutorial). in the Resampling field, select Nearest Neighbour.
3. A popup menu will open up. set the Cell Size field to 1 (or whatever resolution you desire).
4. In the popup menu, press Okay
5. To save your georeferenced image, in the Data tab, right click the image and press Save As.

Congratulations, you have just georeferenced a map in SAGA GIS!

Georeferencing Google Earth Imagery

The process for georeferencing google earth imagery is very similar to georeferencing a historical map or topo sheet. The main differences are as follows:

1. Instead of using graticles for the GCP locations, use the points you created in google earth when collecting the image
2. Google earth uses the WGS84 Datum and the Equidistant Cylindrical (Plate Caree) Projection. Make sure to use these when defining a projection.
3. Google Earth imagery is NOT orthorectified. If you have any points of known location you can use as GCPs, you may want to, as well as a comparison with LANDSAT imagery if possible.

Transformations and Interpolation

Transformations

Because images obtained from aerial photography may be distorted, often it is necessary to apply a Transformation during the georeferencing process. Different transformations are available at the following transformations are available in SAGA GIS

Triangulation

There is no documentation as to which transformation this represents located anywhere online or otherwise

Spline

Spline transformations are optimized for local accuracy at the expense of global accuracy. In a spline transformation, source and target control points are mapped to each other exactly, while pixels that are further away have greater chance of inaccuracy.

This transformation, known as a "rubber sheet" transformation, is of greatest use when the exact location of certain points is of high importance.

Spline transformations require a minimum of 10 GCPs, and adding more points increases the accuracy of a spline transformation

Affine

Affine is a linear transformation that can scale, translate, rotate, and skew an image. An affine transformation generally maintains straight lines, with squares and rectangles becoming parallelograms.

An affine transformation requires at least 3 GCPs, with each additional GCP introducing additional error. However, inaccurate positioning of GCPs has a greater impact on inaccuracy than additional GCPs, therefore more than 3 GCPs should be used.

First Order Polynomial

This option represents similarity transformations, which are similar to affine transformations in that they are linear, 1st order transformations. however, unlike affine translations, similarity transformations are unable to either independently scale the axis or apply any skew. This is useful for the digitization of "as built" schematics.

A similarity transformation requires 2 GCPs. Additional GCPs will produce RMS error

Second Order Polynomial

Second order polynomial transformations, or quadratic transformations, begin to introduce curvature into the shape of the transformed image. citation a 2nd order polynomial transformation applies a simple global curvature to the raster. Citation

A second order polynomial requires 6 GCPs

Third Order Polynomial

Third order polynomial transformations, or cubic transformations, introduce more complex curvature into the shape of a transformed rasterm citation.

A third-order polynomial transformation requires 10 GCPs.

Polynomial, Order

This setting allows you to input a custom order for your polynomial transformation, increasing the complexity of the curve produced

Resampling

When a geometric transformation is applied to a raster, the cells of the input and output rasters rarely line up. To assign values to each output cell, an interpolative algorithm is applied to the input raster, which then assigns values to the initially-empty cells of the output raster. There are 4 methods of interpolation available for resampling in SAGA GIS.

Nearest Neighbour

Nearest Neighbour assigns to the cell of the output raster the closest cell on the input raster to the corresponding output raster cell.

Values in the input raster directly correspond to values in the output raster. there are no changes made to any input raster values.

This method is suitable for nominal and ordinal data, as if the input raster is entirely integer, so too will the output raster. As such, catergories and classes are maintained

Bilinear Interpolation

Bilinear interpolation assigns to the output raster the average of the 4 nearest cells on the input raster to the corresponding output raster call. the average value is weighted to account for distance, with closer cells having relatively more influence than more distant cells.

Bilinear interpolation is valuable for continuous data as it produces a much smoother surface than Nearest Neighbour or Bicubic Spline interpolation.

Bicubic Spline Interpolation

Bicubic Spline interpolation, also known as cubic convolution, assigns to the output raster the distance-weighted average of the nearest 16 cells of the input raster to the corresponding output raster cell.

As more cells are included in the weighted average, the results are sharper and therefore more suited to satelite and aerial photography.

For the same reasons as Bilinear Interpolation, Bicubic Spline interpolation should not be used for categorical data.

citation.

B-Spline Interpolation

B-spline interpolation makes use of a sequence of increasingly fine-scale bicubic functions to approximate the function of a single B-spline function. This functions similarly to B-spline interpolation, but is more computationally efficient. citation