Areal Interpolation in Python Using Tobler

Introduction

Areal interpolation, in vector-based GIS data models, is the process where the attributes of one set of polygons are interpolated to a different set of polygons. There are many applications for this process, for example, the interpolation of census data from census tracts to neighborhoods, or the interpolation of aggregated environment data from one set of geographic boundaries to another.

Tobler, a component of the Python Spatial Analysis Library (PySAL) is a package of Python functions designed to perform and support areal interpolation. Visit Tobler's website and github page for the official documentation.

In this tutorial we will use Tobler to perform two different methods of areal interpolation on two different scales of source data. In Part 1 we will use areal weighted and dasymetric methods to interpolate 2016 Canadian census data from Ottawa census tracts and dissemination areas to Ottawa neighborhoods. In part 2 we will do same but with synthetic population data instead of real data. By using this synthetic dataset we will know exactly what the results should be and thus more accurately assess the effect of the methods and scale.

The intended audience of this tutorial are students who have some prior experience using Python, JupyterLab, Jupyter Notebooks, Pandas, and GeoPandas. That being said, the code should work as-is, providing all students with the opportunity to follow along through the steps of the analysis. If you are new to Jupyter notebooks and need help running code cells or performing other basic operations then check out Project Jupyter's introductory tutorials. I have included links to the different packages' documentation throughout the tutorial and feel free to insert or split cells at any point in order to inspect any intermediate data.

Disclaimer: The tutorial and all related documents have been created as a school assignment for Carleton University's GEOM 4008 – Advanced Topics in Geographic Information Systems course. Please forgive any errors, whether simple typographic ones or more critical errors in logic or syntax. Whether you happened upon this document through its github repository or Carleton University's Open Source GIS Tutorials page and want to propose any changes, feel free to submit a pull request to this tutorial's github repository or find me at my Twitter account.

Getting Started

There are a couple of different ways to access this tutorial. If you wish to interact with it by editing and running the code then the simplest method is through Binder. This service will allow you to run the tutorial notebook in JupyterLab without needing to download anything or creating an environment. Alternatively, you can download the files from the github repository, set up the environment, and run the notebook locally. If a static copy of the tutorial is all you want then feel free to read the through the copy here at at Carleton University's Open Source GIS Tutorials page.Here are the instructions for these three options:

Option 1: Non-Interactive Copy

As mentioned, this tutorial was created as a student project for a Carleton University geomatics course. It has been converted to a MediaWiki page and uploaded to the page you are currently viewing.

Option 2: Run the Tutorial Through Binder

Please follow these instructions if you want to use an online interactive copy of the tutorial:

1. Open this link in a new tab to access a Binder copy of the tutorial repository.
2. While the Binder service is loading, you can access a non-interactive preview of the notebook (areal_interp_tutorial.ipynb) through nbviewer at the bottom of the page.
3. After loading, a JupyterLab session will launch in your browser. This session will use the tutorial environment so all dependencies should work.
4. In the File Browser pane on the left, double-click areal_interp_tutorial.ipynb to open the tutorial notebook.
5. With the tutorial now open as an interactive Jupyter notebook you can run and modify each code cell and any output.

Option 3: Install a Local Copy of the Tutorial

Please follow these instructions if you want to use a local interactive copy of the tutorial:

Step 1: Download the Files

If you have git installed:

1. Open a terminal window
2. Change the current working directory to the location where you want the tutorial to reside
3. Clone the repo by running: $ git clone https://github.com/johnofoster/areal_interpolation_tutorial

Otherwise, simply download the zip file of the tutorial from this link and unzip it into a suitable working directory on your computer.

Step 2: Create Environment

This tutorial uses Python 3.9, Conda, JupyterLab, and a number of Python packages.

If you don't already have an Anaconda distribution then you can find it here. For a very lightweight alternative to Anaconda that only contains Conda, Python, and a few essential packages then check out Miniconda here. After installing either please follow these instructions:

1. Open a terminal window
2. Change the current working directory to tutorial's directory
3. Create the environment by running: $ conda env create -- file environment.yml
4. It might take a while to build the environment so go grab a cup of your favorite beverage.

This will create a Conda environment containing the necessary packages to run this tutorial.

Step 3: Open the Tutorial

Now that you have downloaded the tutorial files and created the Conda environment please follow these instructions to launch it:

1. Open a terminal window
2. Change the current working directory to the tutorial's directory
3. Activate the environment: $ conda activate areal_interp_env
4. Start a local JupyterLab session in your web browser: $ Jupyter Lab
5. In the File Browser pane on the left, double-click areal_interp_tutorial.ipynb to open the tutorial notebook.
6. With the tutorial now open you can run and modify each code cell in order to see the output.

Step 4: Remove the Tutorial

Once you are done with tutorial you might want to remove it. Simply delete the directory you placed it in and then remove the Conda environment by running the following terminal command: $ conda env remove --name areal_interp_env.

Data Sources

The data for this tutorial has been preprocessed for your convenience and can be found in data/. All of this data comes from free and open sources. Links to the original geometry and attributes can be found below along with notes regarding the preprocessing that was performed.

	Geometry source	Geometry transformations	Attributes source	Attributes transformations
Census Tracts	StatCan 2016 Census - Census Tracts Cartographic Boundary File	Extracted the census tracts falling within the City of Ottawa boundary and reprojected to WGS 84 UTM 18N	StatCan 2016 Census: Census metropolitan areas (CMAs), tracted census agglomerations (CAs) and census tracts (CTs)	Extracted the 'Population, 2016' data ('member ID 1') for the City of Ottawa census tracts and joined them to the census tracts geometry
Dissemination Areas	StatCan 2016 Census - Dissemination Areas Cartographic Boundary File	Extracted the dissemination areas falling within the City of Ottawa boundary and reprojected to WGS 84 UTM 18N	Canada, provinces, territories, census divisions (CDs), census subdivisions (CSDs) and dissemination areas (DAs) - Ontario only	Extracted the 'Population, 2016' data ('member ID 1) for the City of Ottawa dissemination areas and joined them to the dissemination areas geometry
Neighborhoods	Ottawa Neighbourhood Study (ONS) - Neighbourhood Boundaries Gen 2	Reprojected to WGS 84 UTM 18N	Ottawa Neighbourhood Study (ONS) - Neighbourhood Boundaries Gen 2	Extracted the neighbourhood names ('NAMES') and estimated population fields ('POPEST')
Landcover	Government of Canada - 2015 Land Cover of Canada	Clipped to the City of Ottawa's extent
Zoning	City of Ottawa - Zoning	Reprojected to WGS 84 UTM 18N	City of Ottawa - Zoning	Extracted the main zones
Synthetic Points	John Foster (tutorial author)

Areal Interpolation in Python Using Tobler - Tutorial

Import Modules and Packages

This tutorial requires the use of a number of modules. Tobler, Pandas, GeoPandas, and Plotly will perform most of the work but see the comments below for why we are importing each.

# Import modules
# --------------

import geopandas as gpd                     # For operations on GeoDataFrames
from IPython.display import display_html    # To display DataFrames side-by-side
import json                                 # For plotting geometries with Plotly
import matplotlib.pyplot as plt             # General purpose plotting
import numpy as np                          # Statistical functions and classes
import pandas as pd                         # For operations on DataFrames
import plotly.express as px                 # For interactive plotting
import tobler                               # For the areal interpolation functions
from scipy import stats                     # For the linear regression function
from shapely.geometry import Point          # For the point geometry class

Part 1 - Areal Interpolation of Census Population Data

Step 1: Read The Data

Before performing any analysis we need read the data files from our data/ directory and assign them to variables. We will do this with GeoPandas' read.file() method.

# Read the data
# -------------

# City of Ottawa census tracts data
ct_gdf = gpd.read_file(filename='data/ottawa_ct_pop_2016.gpkg')

# City of Ottawa dissemination areas data
da_gdf = gpd.read_file(filename='data/ottawa_da_pop_2016.gpkg')

# City of Ottawa neighborhoods data
nbhd_gdf = gpd.read_file(filename='data/ottawa_neighborhoods.gpkg')

Step 2: Inspect the Data

We can use Pandas' df.sample() method to inspect a small random samples of the census tracts, dissemination areas, and neighborhoods GeoDataFrames (while ignoring their geometry columns). This will show us the column names and give us some examples of how the values of each are formatted. Because the output of cells in Jupyter notebooks are rendered in HTML we can use Pandas' DataFrame styling methods to display several DataFrames side-by-side. While this takes more code than simply using the print() function or displaying the results of sample(), it facilitates comparisons and saves vertical space.

# Compare random samples from each GeoDataFrame
# ---------------------------------------------

# Assign a sampling of each GeoDataFrame to a DataFrame
df1 = ct_gdf.drop(columns='geometry').sample(5)
df2 = da_gdf.drop(columns='geometry').sample(5)
df3 = nbhd_gdf.drop(columns='geometry').sample(5)

# Style the DataFrames and include captions with the number of rows
style = "style='display:inline; padding:10px'"
df1_styled = df1.style.set_table_attributes(style).set_caption(f'Census Tracts, {len(ct_gdf)} rows')
df2_styled = df2.style.set_table_attributes(style).set_caption(f'Dissemination Areas, {len(da_gdf)} rows')
df3_styled = df3.style.set_table_attributes(style).set_caption(f'Neighborhoods, {len(nbhd_gdf)} rows')

# Display the three DataFrames
display_html(df1_styled._repr_html_() + df2_styled._repr_html_() + df3_styled._repr_html_(), raw=True)

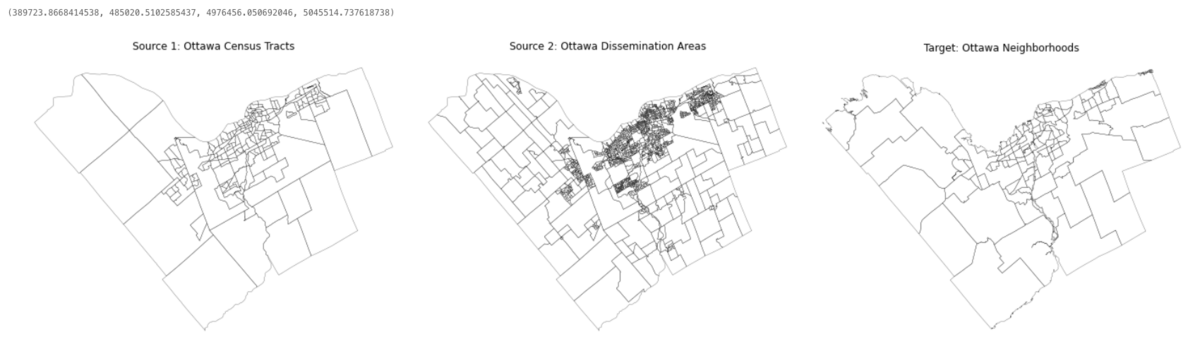
From this we can see that the census tracts and neighborhoods have roughly similar population values but the dissemination areas are quite a bit smaller.

For a quick spatial inspection let's plot the geometries of each GeoDataFrame next to each other using Matplotlib's subplots and GeoPandas' plot() methods. This will reveal the scale and shape of the geometries that we are working with.

# Plot the target and source geometries
# -------------------------------------

# Create subplots; set their size and padding
fig, axs = plt.subplots(nrows=1, ncols=3, figsize=(25, 25))
plt.subplots_adjust(wspace=0)

# Plot the Ottawa census tracts figure
ct_gdf.plot(ax=axs[0], color="none", linewidth=0.25)
axs[0].set_title('Source 1: Ottawa Census Tracts')
axs[0].axis('off')

# Ottawa dissemination areas figure
da_gdf.plot(ax=axs[1], color="none", linewidth=0.25)
axs[1].set_title('Source 2: Ottawa Dissemination Areas')
axs[1].axis('off')

# Ottawa neighborhoods figure
nbhd_gdf.plot(ax=axs[2], color="none", linewidth=0.25)
axs[2].set_title('Target: Ottawa Neighborhoods')
axs[2].axis('off')

Additional Methods for Inspecting Data

The following Pandas and GeoPandas methods are great ways to inspect DataFrames and GeoDataFrames.

• df.info(): Information about the DataFrame/GeoDataFrame such as column names, data types, and length
• df.head(): First n rows of the DataFrame/GeoDataFrame (defaults to 10 rows)
• df.tail(): Last n rows of the DataFrame/GeoDataFrame (defaults to 10 rows)
• df.sample(): Random sample of n rows of the DataFrame/GeoDataFrame (defaults to 1 rows)
• gdf.explore(): Interactive map of a GeoDataFrame
• gdf.crs: Coordinate reference system information of a GeoDataFrame

The DataFrame (df) methods also work on GeoDataFrames (gdf) but explore() only works with GeoDataFrames. Follow their links to see the documentation as their outputs can be controlled by passing different arguments to them.

The cell below contains these data inspection methods. Just replace df or gdf before the dot notation with the DataFrame or GeoDataFrame's name that you want to inspect. For example:

• ct_gdf.info() - shows info about the census tracts GeoDataFrame
• da_gdf.explore(column='da_pop_2016') - displays an interactive map of the dissemination areas with a colormap of the population column

Alternatively, feel free to insert or split cells at any point in this tutorial in order to inspect intermediate data. These methods will really help to reveal exactly what is going on.

# Data inspection methods
# ----------------

# Uncomment individual lines below and replace `df` or `gdf` with the name of the variable
# DataFrame (df) methods work on GeoDataFrames (gdf) but not the other way around

# df.info()
# df.head()
# df.tail(5)
# df.sample(15)
# gdf.explore()
# gdf.crs

Step 3: Areal Interpolation of Census Data

Now that we have an understanding of the data we're working with we can move on to the area weighted and dasymetric interpolation.

Area Weighted Interpolation

Area weighted interpolation works by intersecting the source and target geometries, calculating the areal weights (i.e. the proportion a source geometry is covered by each given target geometry), and then allocating a proportional amount of the variable from the source to the targets. Please refer to Tobler's documentation of the tobler.area_weighted.area_interpolate() function for a mathematical description and help with the parameters.

The first thing to consider is whether the variable to be interpolated is extensive or intensive. An extensive variable is one that depends on the size of the sample (e.g. population counts) while an intensive variable does not (e.g. population density). In this tutorial we will only be working with extensive variables (population counts) but it's worth noting that Tobler's interpolation methods can handle both types through the use of different parameters.

As mentioned, the areal interpolation operation will be performed twice: first with the census tracts as the source data, then with the dissemination areas. This will allow us to compare the results of these different source geometries to see if there's any benefit gained by using smaller census geographies (i.e. dissemination areas) as the source.

To use the tobler.area_weighted.area_interpolate() function we will pass source and target GeoDataFrames to it along with the column name of the extensive variable. The extensive variable will then be interpolated from the source geometry to the target geometry. The result will be a GeoDataFrame containing the target geometries and interpolated values of the extensive variable. After running these cells there will be no output but the results will be saved to the ct_area_interp_gdf and da_area_interp_gdf variables. These will be plotted once all four interpolation operations have been completed.

It's important to note that these three spatial dataset have already been reprojected into the WGS 84 / UTM 18N (EPSG:32618) CRS. If you use Tobler with your own GeoDataFrames it's recommended to explicitly reproject the data into an appropriate UTM zone beforehand, even though Tobler will try to do this automatically. Reprojecting a GeoDataFrame is easily accomplished with the gdf.to_crs() method.

# Area weighted interpolation: census tracts to neighborhoods
# -----------------------------------------------------------

ct_area_interp_gdf = tobler.area_weighted.area_interpolate(source_df=ct_gdf, 
                                                        target_df=nbhd_gdf,
                                                        extensive_variables=['ct_pop_2016'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
ct_area_interp_gdf['ct_pop_2016'] = ct_area_interp_gdf['ct_pop_2016'].round(decimals=0).astype(int)

# Rename the results column for clarity later
ct_area_interp_gdf = ct_area_interp_gdf.rename(columns={'ct_pop_2016':'ct_area_interp_est'})

# Area weighted interpolation: dissemination areas to neighborhoods
# -----------------------------------------------------------------

da_area_interp_gdf = tobler.area_weighted.area_interpolate(source_df=da_gdf, 
                                                        target_df=nbhd_gdf,
                                                        extensive_variables=['da_pop_2016'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
da_area_interp_gdf['da_pop_2016'] = da_area_interp_gdf['da_pop_2016'].round(decimals=0).astype(int)

# Rename the results column for clarity later
da_area_interp_gdf = da_area_interp_gdf.rename(columns={'da_pop_2016':'da_area_interp_est'})

Dasymetric Interpolation of Census Tracts and Dissemination Areas

Dasymetric interpolation, or masked area weighted interpolation, incorporates secondary information to help refine the spatial distribution of the variable. For example, the extent of census tracts may include large portions of land that are uninhabited (e.g. parks, fields, water, etc.). Secondary information about the census tracts' land cover is used to mask out those uninhabited areas which don't contain the extensive variable. Area weighted interpolation is then applied to the masked census tracts and the results should be more accurate than simple area weighted interpolation on its own. This can be done by clipping the census tracts using another set of appropriate polygons(e.g. land cover polygons, municipal zoning, etc.) and then running the areal interpolation function, but Tobler includes a function to do this automatically using a land cover raster as the secondary information. Please refer to Tobler's documentation of the tobler.dasymetric.masked_area_interpolate()](https://pysal.org/tobler/generated/tobler.dasymetric.masked_area_interpolate.html#tobler.dasymetric.masked_area_interpolate) function for help with the parameters.

The land cover raster that we will use comes from the 2015 Land Cover of Canada. This 30 m spatial resolution land cover product is produced every 5 years and covers the whole country. Tobler's dasymetric interpolation function will automatically clip the raster to the extent of the source data (City of Ottawa) but I have already clipped it to reduce the file-size and processing time.

The path of the land cover raster and the pixel value(s) of the land cover classes that contain dwellings are passed to the function along with the source and target GeoDataFrames, and the column name of the extensive variable. The result is a GeoDataFrame made up of the target geometries with interpolated values for the extensive variable.

For the same reason as before, we will perform the dasymetric interpolation twice: first with the census tracts as the source data, and then with the dissemination areas. masked_area_interpolate() will throw some warnings but just ignore them. The length of time it takes to run each of these cells on my computer has been included for your reference.

# Dasymetric interpolation: census tracts + urban landover to neighborhoods
#--------------------------------------------------------------------------

# Perform dasymetric interpolation
ct_dasy_interp_gdf = tobler.dasymetric.masked_area_interpolate(source_df=ct_gdf, 
                                                            target_df=nbhd_gdf,
                                                            raster='data/ottawa_landcover.tif',
                                                            codes=[17],
                                                            extensive_variables=['ct_pop_2016'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
ct_dasy_interp_gdf['ct_pop_2016'] = ct_dasy_interp_gdf['ct_pop_2016'].round(decimals=0).astype(int)

# Rename the results column for clarity later
ct_dasy_interp_gdf = ct_dasy_interp_gdf.rename(columns={'ct_pop_2016':'ct_dasy_interp_est'})

# ~30 s ; ignore warnings

# Dasymetric interpolation: dissemination areas + urban landover to neighborhoods
#------------------------------------------------------------------------

# Perform dasymetric interpolation
da_dasy_interp_gdf = tobler.dasymetric.masked_area_interpolate(source_df=da_gdf, 
                                                            target_df=nbhd_gdf,
                                                            raster='data/ottawa_landcover.tif',
                                                            codes=[17],
                                                            extensive_variables=['da_pop_2016'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
da_dasy_interp_gdf['da_pop_2016'] = da_dasy_interp_gdf['da_pop_2016'].round(decimals=0).astype(int)

# Rename the results column for clarity later
da_dasy_interp_gdf = da_dasy_interp_gdf.rename(columns={'da_pop_2016':'da_dasy_interp_est'})

# ~1.5 mins : ignore warnings

Step 4: Assess the Interpolation Results

Because the Ottawa Neighbourhood Study data came with a population estimate for each neighborhood (nbhd_pop_est) we can compare those original estimated values against the interpolated values. That being said, it's important to note that the accuracy of this assessment will be very limited for a number of reasons:

1. Metadata associated with the Ottawa neighborhood survey data does not specify the year of their population estimates. This data was first published to the Open Ottawa data portal on November 25, 2019 and then updated on June 2, 2021. The census tract and dissemination area population data comes from the 2016 census.
2. Metadata associated with the Ottawa neighborhood survey data does not specify the methodology they used for estimating the neighborhood populations. Perhaps it comes from an areal interpolation method similar to what we are using or perhaps from a higher resolution data set that is not public (e.g. size of each households).
3. The Ottawa neighborhood survey data indicates that the 'Beechwood Cemetery' and 'Notre-Dame Cemetery' neighborhoods have populations of 139 and 17, respectively, despite no evidence of residences within them.
4. The sum of all the neighborhood population estimates is 867146 while the census_tracts' sum is 934243. These last two points suggest that these neighborhood population estimates are the result of interpolation from an unknown dataset (2011 census data perhaps?).

Despite these issues we will go ahead and use these estimates to assess the interpolation results. We will do the following:

1. Merge the interpolation results with the neighborhood population estimates so we can compare a sample of the results
2. Perform a statistical assessment of the interpolation results
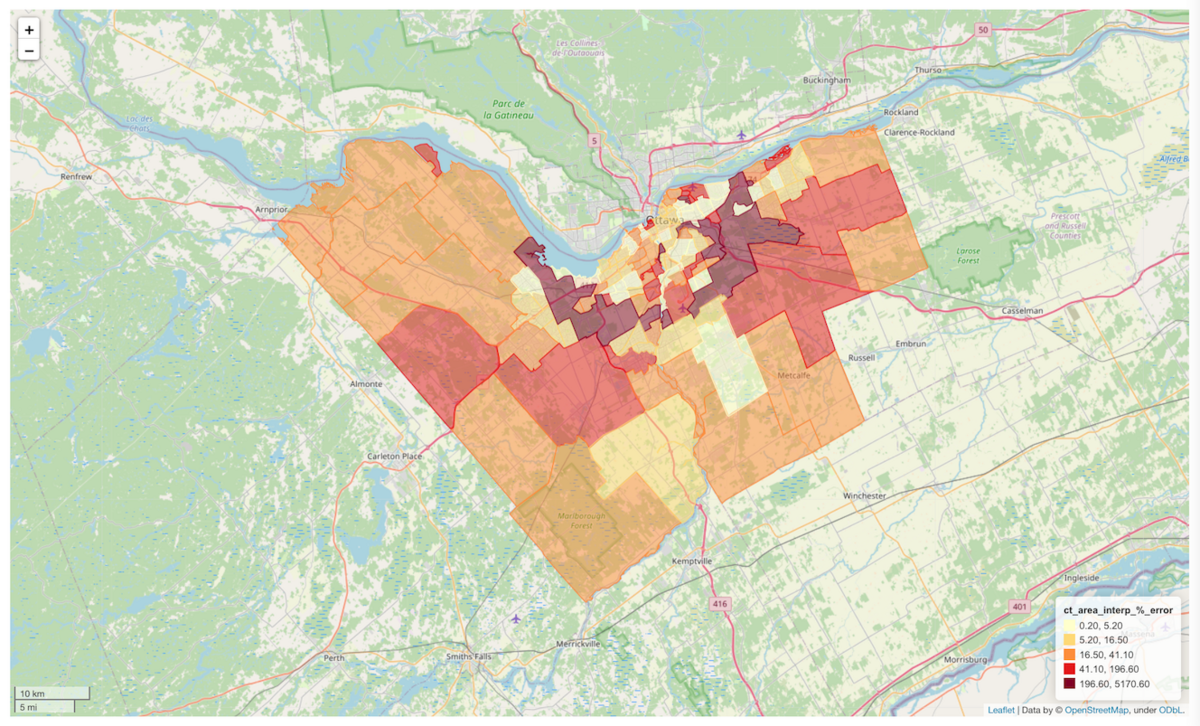
3. Visually assess the percent error of each neighborhood (interpolated population vs nbhd_pop_est) as a map
4. Create a 1:1 scatter plot of the interpolation results against the neighborhood population estimates
5. Discuss the results

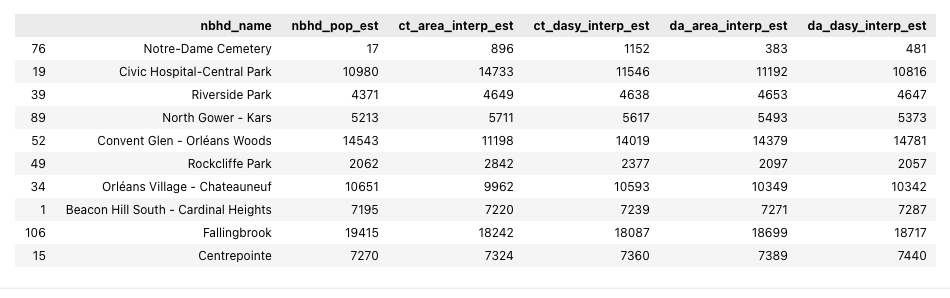
# Merge the results for comparison
#---------------------------------

# Create a list of the GeoDataFrames (dropping the redundant geometry)
dfs = [nbhd_gdf,
        ct_area_interp_gdf.drop(columns='geometry'),
        ct_dasy_interp_gdf.drop(columns='geometry'),
        da_area_interp_gdf.drop(columns='geometry'),
        da_dasy_interp_gdf.drop(columns='geometry')]

# Concatenate the GeoDataFrames
interp_results_gdf = pd.concat(objs=dfs, axis=1)

# View a sample of the interpolation results GeoDataFrame (without the geometry column)
interp_results_gdf.sample(10).drop(columns='geometry')

Looking at this sample we can see that the different interpolation methods and source data have yielded results that look roughly in line with the neighborhood population estimates that came from the Ottawa Neighbourhood Study data (nbhd_pop_est).

Let's continue with our evaluation while not forgetting that the neighborhood population estimates have some issues. We will begin by defining some functions to calculate percent error, root mean square error, normalized square error, mean bias error, mean absolute error, and r value. There are 3rd party modules that contain functions to perform these calculations but defining our own is a good exercise.

# Define functions to assess the results
# --------------------------------------

# Percent error
def percent_error(estimated, expected):
    ''' Return Percent Error where estimated and expected are numeric or array-like'''
    return abs(((estimated - expected) / expected) * 100)

# Root mean square error
def rmse(estimated, expected):
    ''' Return Root Mean Square Error where estimated and expected are array-like'''
    return np.sqrt(np.mean((estimated - expected) ** 2))

# Normalized root mean square error based on standard deviation
def nrmse(estimated, expected):
    ''' Return Normalized Root Mean Square Error where estimated and expected are array-like'''
    return np.sqrt(np.mean((estimated - expected) ** 2))/np.std(estimated)

# Mean bias error
def mbe(estimated, expected):
    ''' Return Mean Bias Error where estimated and expected are array-like'''
    return np.mean(estimated - expected)

# Mean absolute error
def mae(estimated, expected):
    ''' Return Mean Mean Absolute Error where estimated and expected are array-like'''
    return np.mean(abs(estimated - expected))

# r value
def r_value(estimated, expected):
    ''' Return r value where estimated and expected are array-like.'''

    # Get the r_value by unpacking the results from SciPy's linregress() function
    slope, intercept, r_value, p_value, std_err = stats.linregress(estimated, expected)
    return r_value

We will now use those functions to generate statistics on the four sets of interpolation results. The percent error values are concatenated to the interp_results_gdf so we can plot maps showing the percent error of each neighborhood. The other statistics are placed into their own DataFrame so we can assess them in a tabular format.

# Calculate statistics on the interpolation results
# -------------------------------------------------

# Assign the interpolation results columns to their own variables for clarity
ct_area_est = interp_results_gdf['ct_area_interp_est'] # Source: census tracts | method: area weighted
ct_dasy_est = interp_results_gdf['ct_dasy_interp_est'] # Source: census tracts  method: dasymetric
da_area_est = interp_results_gdf['da_area_interp_est'] # Source: dissemination areas | method: area weighted
da_dasy_est = interp_results_gdf['da_dasy_interp_est'] # Source: dissemination areas | method: dasymetric
expected = interp_results_gdf['nbhd_pop_est']          # Source: neighborhoods

# Create new columns in interp_results_gdf to represent percent error
interp_results_gdf['ct_area_interp_%_error'] = round(percent_error(ct_area_est, expected), 1)
interp_results_gdf['ct_dasy_interp_%_error'] = round(percent_error(ct_dasy_est, expected), 1)
interp_results_gdf['da_area_interp_%_error'] = round(percent_error(da_area_est, expected), 1)
interp_results_gdf['da_dasy_interp_%_error'] = round(percent_error(da_dasy_est, expected), 1)

# Create a DataFrame containing the other statistics
interp_stats_df = pd.DataFrame(data={'Interpolation Method': ['Area Weighted','Area Weighted',
                                                        'Dasymetric', 'Dasymetric'],
                                'Source Geographies': ['Census Tracts', 'Dissemination Areas',
                                                       'Census Tracts', 'Dissemination Areas'],
                                'RMSE': [rmse(ct_area_est, expected),
                                        rmse(da_area_est, expected),
                                        rmse(ct_dasy_est, expected),
                                        rmse(da_dasy_est, expected)],
                                'NRMSE': [nrmse(ct_area_est, expected),
                                        nrmse(da_area_est, expected),
                                        nrmse(ct_dasy_est, expected),
                                        nrmse(da_dasy_est, expected)],            
                                'MBE': [mbe(ct_area_est, expected),
                                        mbe(da_area_est, expected),
                                        mbe(ct_dasy_est, expected),
                                        mbe(da_dasy_est, expected)],
                                'MAE': [mae(ct_area_est, expected),
                                        mae(da_area_est, expected),
                                        mae(ct_dasy_est, expected),
                                        mae(da_dasy_est, expected)],
                                'r': [r_value(ct_area_est, expected),
                                        r_value(da_area_est, expected),
                                        r_value(ct_dasy_est, expected),
                                        r_value(da_dasy_est, expected)],
                                'r2': [r_value(ct_area_est, expected)**2,
                                        r_value(da_area_est, expected)**2,
                                        r_value(ct_dasy_est, expected)**2,
                                        r_value(da_dasy_est, expected)**2]}).round(decimals=2)

# Display the DataFrame containing the statistics
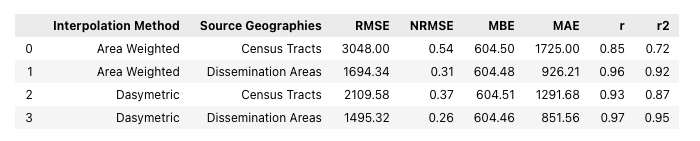
interp_stats_df

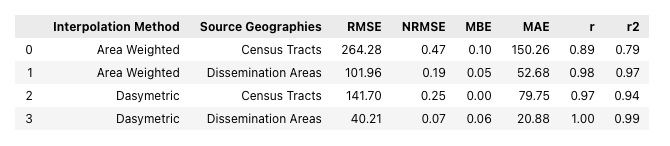
From these statistics it's pretty clear that, when comparing the results from the same source data, the dasymetric method is more effective than the area weighted method. This is shown by the lower error values (as represented by the RMSE, NRMSE, and MAE) and higher correlations (r values) achieved by the dasymetric method.

Interestingly, these statistics also show that using the relatively small dissemination areas as the source data yields the lowest errors and highest correlations - regardless of the interpolation method. This makes sense, as the dissemination areas are much smaller than the census tracts, giving a higher spatial resolution of data for the re-aggregation of the extensive variable from the source to the target geometries. The 'masking' approach that the dasymetric method uses can be seen as an attempt to mimic a higher spatial resolution source dataset, in both cases improving the results compared to the simple area weighted method.

Positive MBE values for all four interpolation results show that all four interpolation results are coming out higher than the neighborhood population estimates. As previously discussed, this is due to a higher total population in the census data (934243) than in the neighborhood data (867146). It's too bad these neighborhood estimates aren't closer to the census data as that would help to make this assessment more credible.

Let's see if a visual assessment of the results line up with this statistical one. Plotly offers a very powerful set of plotting tools which render spatial and non-spatial data as interactive figures. There are simpler ways to plot this with less code but the interactive nature of these Plotly figures is really great for exploratory data analysis. Before creating the Plotly choropleth facet plots the data needs to be reworked into a specific format. The geometries have be supplied in the GeoJson format and the values have to be melted into a single column with an additional column providing labels.

Check out these links for information on the Pandas df.melt() method and Plotly choropleth and facet plots:

• df.melt() documentation
• Plotly Choropleth Maps
• px.choropleth() documentation
• Plotly Facet Plots

# Plot the Percent Error of the four results using a Plotly Facet Map

# --------------------------------------------------------------------------------

# Convert interp_results_gdf from GeoDataFrame to GeoJson
geojson = interp_results_gdf.to_crs(epsg='4326').to_json()
geojson = json.loads(geojson)

# Reformat the interp_results_gdf for the plot
df = pd.DataFrame(data=interp_results_gdf.drop(columns='geometry'))

# Rename the results columns as they will become the facet plot labels
df = df.rename(columns={'ct_area_interp_%_error':'Source: Census Tracts <br> Method: Area Weighted',
                    'ct_dasy_interp_%_error':'Source: Census Tracts <br> Method: Dasymetric',
                    'da_area_interp_%_error':'Source: Dissemination Areas <br> Method: Area Weighted',
                    'da_dasy_interp_%_error':'Source: Dissemination Areas <br> Method: Dasymetric',})

# Combine all the results columns into one column labeled with a method column
df = df.melt(id_vars='nbhd_name',
            value_vars=['Source: Census Tracts <br> Method: Area Weighted',
                        'Source: Census Tracts <br> Method: Dasymetric',
                        'Source: Dissemination Areas <br> Method: Area Weighted',
                        'Source: Dissemination Areas <br> Method: Dasymetric'],
            var_name='method', 
            value_name='Error (%)')

# Create the Plotly Express choropleth figure
fig = px.choropleth(data_frame=df,
                    title="Areal Interpolation of 2016 Census Population Data to Ottawa, ON Neighborhoods",
                    locations='nbhd_name',
                    geojson=geojson,
                    featureidkey='properties.nbhd_name',
                    color='Error (%)',
                    facet_col='method',
                    facet_col_wrap=2,
                    hover_name='nbhd_name',
                    range_color=[0,100],
                    color_continuous_scale='Inferno',
                    #color_discrete_sequence= px.colors.sequential.Plasma,
                    projection='mercator',
                    fitbounds="locations",
                    height=800, width=800)

fig.update_layout(mapbox_style="open-street-map")
fig.for_each_annotation(lambda a: a.update(text=a.text.split('=')[-1]))

fig.show()

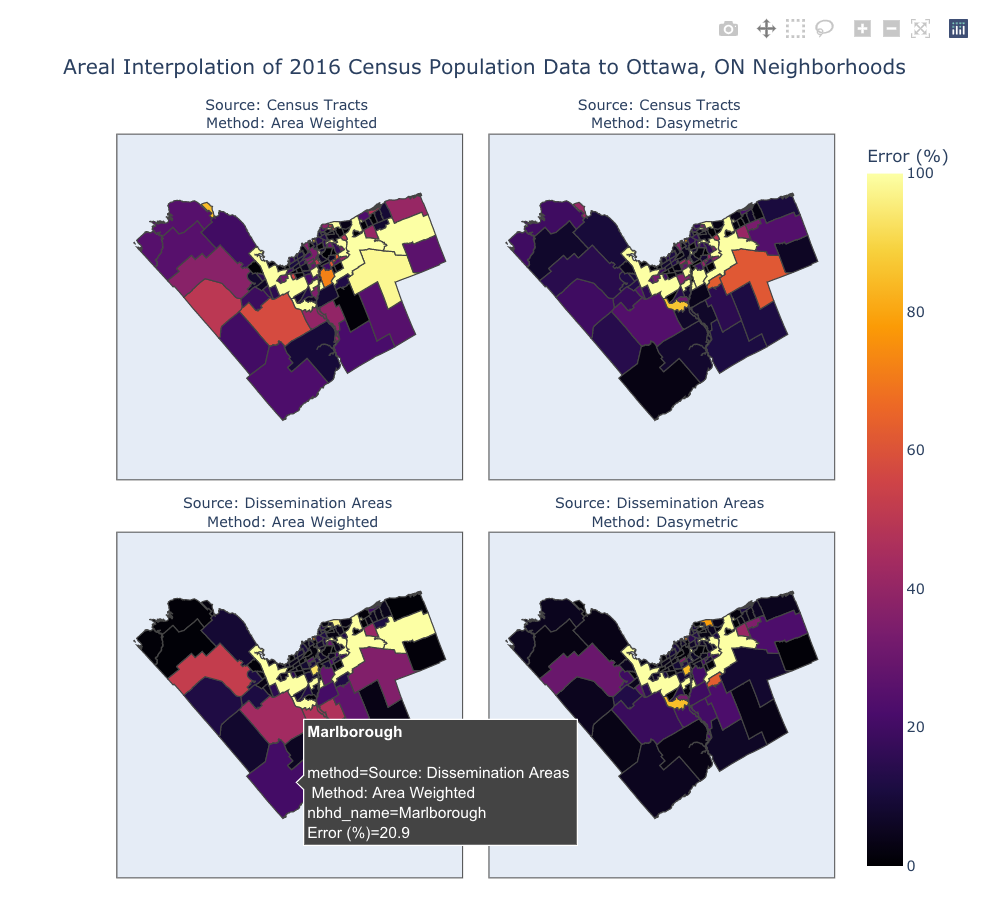
That's a pretty slick set of maps, if I can say so myself! Each map can be explored by changing the zoom level and by hovering the cursor over different features (if you're viewing the interactive Jupyter notebook version of this tutorial).

There are some other limitations with Plotly though. While it does support tiled base maps through their MapBox figures (e.g., px.choropleth_mapbox()) it's not possible to create facet plots (i.e., side-by-side plots) with a tiled base map. Also, Plotly doesn't make it easy to represent the values as discrete classified bins instead of a continuous color scale. Instead, in the map above I've simply limited the Error (%) color bar range to 100 despite some neighborhoods having higher percent errors higher than 100. Feel free to adjust the rangecolor= argument to a different scale, if you so desire.

Another way to represent the results in an interactive map is through GeoPandas' explore() method. Like the Plotly maps, it's possible to change the zoom and inspect attributes of each feature by hovering the cursor over them. There's probably a way to organize these into subplots but I haven't figured that out yet.

In the cell below we can change the column argument to display a color-scaled representation of any of the columns in the interp_results_gdf. The classification scheme can also be changed using the scheme argument. See the gdf.explore() documentation for the classification schemes and other parameters.

# Visually Assess Percent Error of the Area Weighted Interpolation
# ----------------------------------------------------------------

# Uncomment one of the following percent error columns to display that its values in the map
column = 'ct_area_interp_%_error' # Source: Census Tracts | Method: Area Weighted
#column='da_area_interp_%_error' # Source: Dissemination Areas | Method: Area Weighted
#column='ct_dasy_interp_%_error' # Source: Census Tracts | Method: Dasymetric
#column='da_dasy_interp_%_error' # Source: Dissemination Areas | Method: Dasymetric

interp_results_gdf.explore(column=column,
    cmap='YlOrRd',
    scheme='JenksCaspall',
    legend_kwds={'colorbar':False},
    style_kwds={'weight':1})

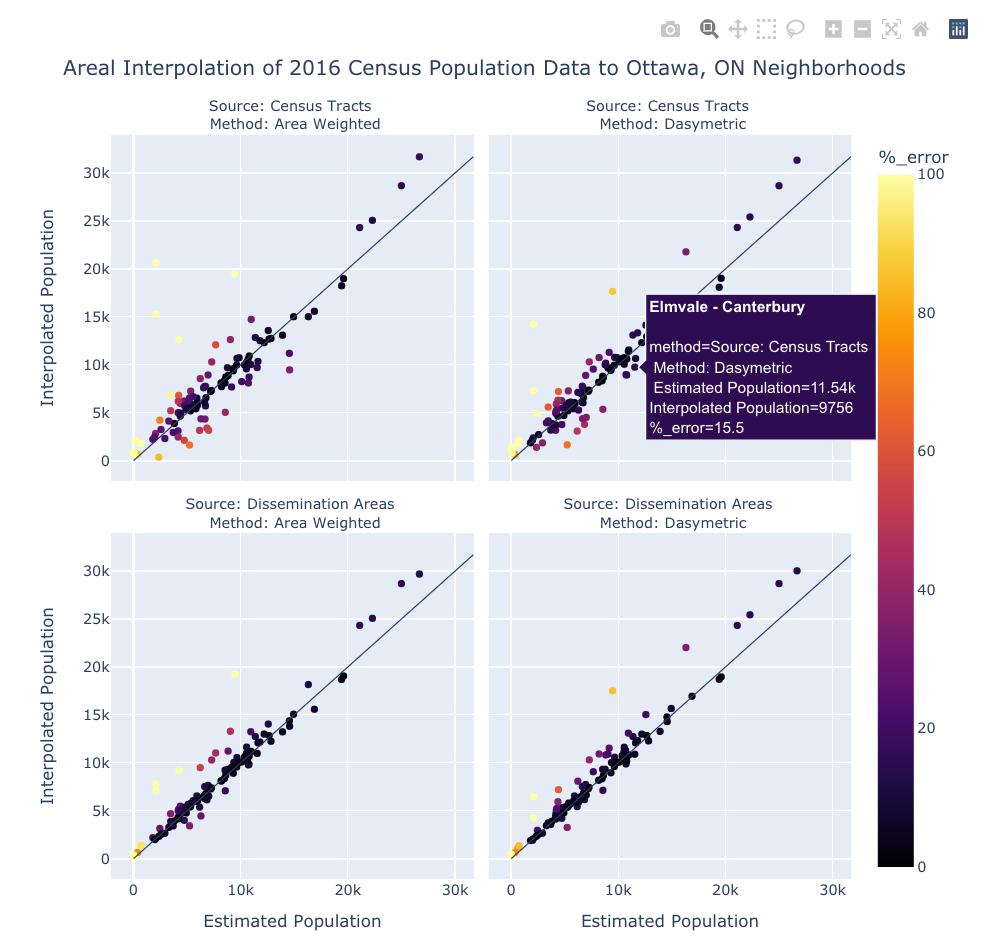
Lastly, let's plot the interpolation results against the neighborhood population estimates using 1:1 scatter plots. We'll use Plotly again for this as its px.scatter() facet plots allow us to hover the cursor over the points in order to see their names and other information. Like the choropleth facet maps , the data needs to be reworked into the correct format using df.melt(). It's a lot of code but I think it's worth it.

Check out these links for information on Plotly scatter plots:

• Plotly Scatter Plots
• px.scatter() documentation

# Create 1:1 Facet Plots using Plotly
# -------------------------------------

# Convert the interpolation results to a DataFrame
df = pd.DataFrame(data=interp_results_gdf.drop(columns='geometry'))

# Rename the results columns as they will become the facet plot labels
df = df.rename(columns={'ct_area_interp_est':'Source: Census Tracts <br> Method: Area Weighted',
                    'ct_dasy_interp_est':'Source: Census Tracts <br> Method: Dasymetric',
                    'da_area_interp_est':'Source: Dissemination Areas <br> Method: Area Weighted',
                    'da_dasy_interp_est':'Source: Dissemination Areas <br> Method: Dasymetric'})

# Combine all the results columns into one column
df = df.melt(id_vars=['nbhd_name', 'nbhd_pop_est'],
            value_vars=['Source: Census Tracts <br> Method: Area Weighted',
                        'Source: Census Tracts <br> Method: Dasymetric',
                        'Source: Dissemination Areas <br> Method: Area Weighted',
                        'Source: Dissemination Areas <br> Method: Dasymetric'],
            var_name='method', 
            value_name='interp_pop_est')

# Add a percent error column
estimated = df['interp_pop_est']
expected = df['nbhd_pop_est']
df['%_error'] = round(percent_error(estimated, expected), 1)

# Create the Plotly Express Scatter figure
fig = px.scatter(data_frame=df,
                title="Areal Interpolation of 2016 Census Population Data to Ottawa, ON Neighborhoods",
                x='nbhd_pop_est',
                y='interp_pop_est',
                height=800, width=800,
                color='%_error',
                facet_col='method',
                facet_col_wrap=2,
                hover_name='nbhd_name',
                labels={'interp_pop_est': 'Interpolated Population',
                        'nbhd_pop_est': ' Estimated Population'},
                color_continuous_scale='Inferno',
                range_color=[0,100])

# Create the 1:1 line
line_max = max([max(df['interp_pop_est']), max(df['nbhd_pop_est'])])
line_min = min([min(df['interp_pop_est']), min(df['nbhd_pop_est'])])

fig.update_layout(shapes=[
        dict(type='line', xref='x', yref='y',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1),
        dict(type='line', xref='x2', yref='y2',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1),
        dict(type='line', xref='x3', yref='y3',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1),
        dict(type='line', xref='x4', yref='y4',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1)])

fig.for_each_annotation(lambda a: a.update(text=a.text.split('=')[-1]))

fig.show()

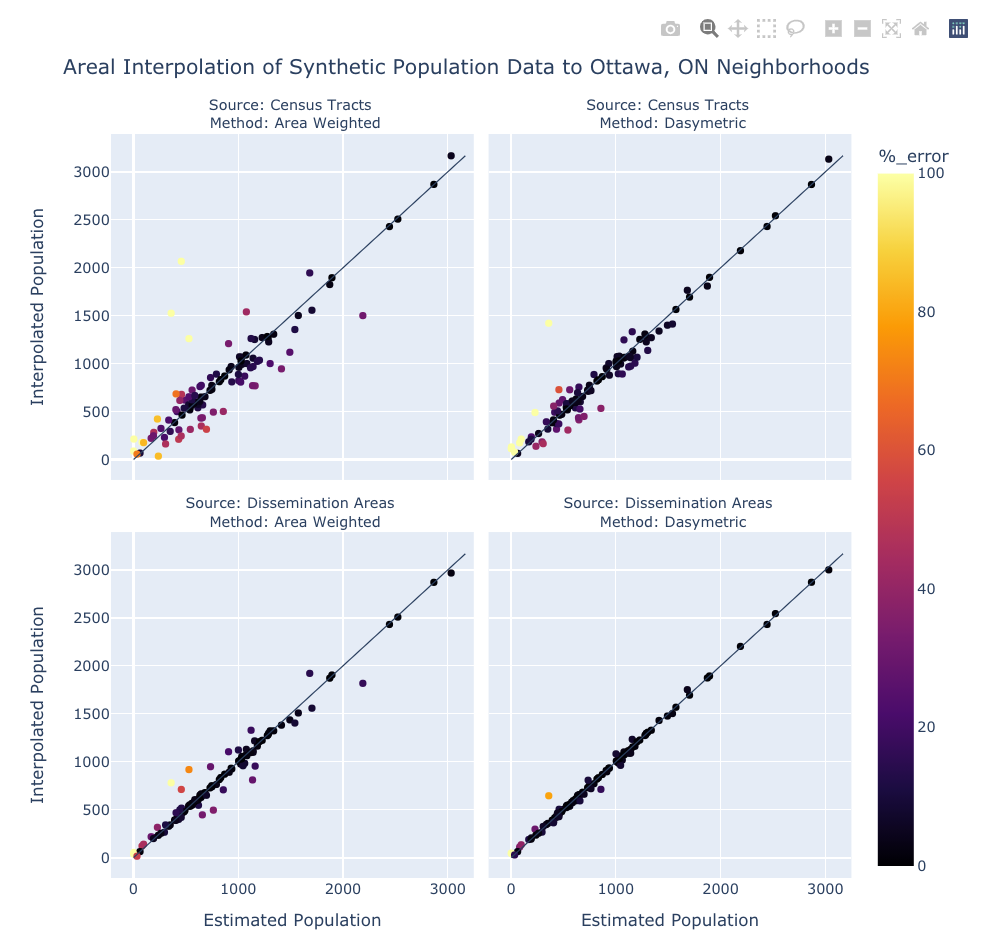
From these plots and maps we can see some shared characteristics of the results:

• They all struggle with the Greenbelt neighborhood. This might be because it's quite large and borders many other neighborhood, or perhaps the census population data and the neighborhood population estimates diverge significantly over this area.
• Neighborhoods with small populations (e.g., Carleton University, Beechwood Cemetary, Notre-Dame Cemetary, Lebreton Development) show high percent errors, possibly due to having low populations while being surrounded by neighborhoods with high populations.
• Neighborhoods with high populations, (e.g.,Stittsville, Centretown, Old Barrhaven East and "Bridlewood - Emerald Meadows") have interpolated populations that are consistently higher than the neighbourhood population estimates. Again, this might be due to underlying issues with the neighbourhood population estimates.
• "Stonebridge - Half Moon Bay - Heart's Desire" has a high percent error in all results - possibly due to the same issue as above.

From this one analysis, and again bearing in mind the issues with the neighborhood population estimates, it's pretty clear that the dasymetric interpolation methods is superior to the area weighted method but high resolution source data has an even more powerful contribution to the accuracy of the results.

So how can we eliminate the issues with the Ottawa Neighborhood Study population estimates and perform a more objective evaluation of the methods? Well, we can make our own population data!

Part 2 - Areal Interpolation of Synthetic Population Data

In part 2 we will perform the same set of areal interpolations but this time the real population data will be replaced with synthetic population data. By doing this we will know the exact population of the census tracts, dissemination areas, and neighborhoods - allowing us to accurately compare the interpolated populations against the expected populations. A better picture should emerge of the differences between the area weighted and dasymetric interpolation methods, and the effect of the source data's scale.

Our steps in part 2 will be:

1. Generate the synthetic population points
2. Count the synthetic population points
3. Perform interpolation
4. Assess the results

Step 1: Create the Synthetic Population Points

We first need to generate a dataset containing a synthetic population. Ideally, we would have access to a dataset where every person in Ottawa is identified as a point at their dwelling but, because StatCan doesn't release this fine scale for privacy reasons, we will have to approximate it.

What we want to do is create a distribution of points that does a pretty good job of approximating the actual distribution of people within a city. It has to have a non-uniform density and be spatially limited to those areas where people actually live. Datasets that could help to approximate this include city land use zones, building footprints, and high resolution land cover maps. To keep things relatively simple here we will just do the following:

1. Clip the dissemination areas to the urban land cover type
   • Tobler provides a handy function that extracts specific land cover types from a raster and then outputs a GeoDataFrame containing their extent: tobler.dasymetric.extract_raster_features()
2. Clip the clipped dissemination areas to Ottawa's land use zones which permit dwellings
   • These land use zones come from Section 35 of the City of Ottawa's zoning definitions
   • Nineteen zones where dwelling units are permitted have been selected (see the code cell below)
   • A more rigorous approach would consider all of the exceptions granted in the subzones but those exceptions will be ignored here
3. Generate a number of randomly distributed points within each dissemination area where the number of those points are based off of the 2016 census population. We don't have to based these numbers off the 2016 census data but it will help to produce a realisitc density
4. Count the number of points that fall within each census tract, dissemination area, and neighborhood

Generating a reasonably large population of synthetic points within these clipped dissemination areas can take quite a long time (about 15 mins for 93433 points on my old MacBook Pro). If you want to avoid the processing time just run the cell immediately below this one ("Skip the point generation and just read them from a file") and then jump ahead to the cell called "Count the points in each census tract". Or, if you want to make your own points then skip the next cell and run all of the others.

Ok, let's get to it.

# Skip the point generation and just read them from a file
# --------------------------------------------------------

points_gdf = gpd.read_file('data/points.gpkg')

# Optional: uncomment the line below to explore the points
#points_gdf.explore()

# Create clipped dissemination areas
# ----------------------------------

# Extract the urban landcover (pixel value of 17) from the landcover raster
raster_path = 'data/ottawa_landcover.tif'
urban_landcover_gdf = tobler.dasymetric.extract_raster_features(gdf=nbhd_gdf,
                                                                raster_path=raster_path,
                                                                pixel_values=17)

urban_landcover_gdf = urban_landcover_gdf.to_crs(epsg=32618)

# Read the Ottawa zoning
zoning_gdf = gpd.read_file('data/ottawa_zoning.gpkg')

# Only keep the zones that residents can live in
people_zones = ['R1', 'R2', 'R3', 'R4', 'R5', 'RM', 'LC', 'GM', 'TM',
                'AM','MC','MD', 'AG', 'RR','RU','VM', 'V1','V2','V3']

zoning_gdf = zoning_gdf[zoning_gdf['zone_main'].isin(people_zones)]

# Clip the dissemination areas to the urban landcover and the zoning
da_clip_gdf = gpd.clip(gdf=da_gdf, mask=zoning_gdf)
da_clip_gdf = gpd.clip(gdf=da_clip_gdf, mask=urban_landcover_gdf)

# ~2 mins ; ignore warnings

# Define function to generate a specific number of random points in a polygon
# ---------------------------------------------------------------------------

def random_points(row, n_column, geom_column, divisor=1, min_n=1):
    ''' Returns n number of random points within GeoDataFrame polygons.

    Parameters:
    ----------
    row : Pandas Series
        Must contain:
        - A column containing the desired number of points in each polygons
        - A column containing polygon geometry

    n_column : string
        - The name of the column that contains the desired number of points

    geom_column : string
        - The name of the column that contains the GeoDataBase geometry

    divisor : int (default = 1)
        - A value used to reduce the number of points (n2 = n1 / divisor)
        - Good for shortening computation time

    min_n : int (default = 1)
        - The minimum number of points in polygon
        - Good for forcing all polygons to have at least 1 point

    Notes:
    ------
    This function is very very slow when trying to generate points in polygons that
    have areas that are much smaller than their extent (e.g a C-shaped polygon)
    '''
    
    # Read the polygon and its bounds
    polygon = row[geom_column]
    min_x, min_y, max_x, max_y = polygon.bounds

    # Determine the number of points to generate in the polygon
    n_points = round((row[n_column] / divisor), 0)
    if n_points < min_n:
        n_points = min_n
    
    # Generate the points and put them in a list
    points_list = []
    while len(points_list) < n_points:
        point = Point(np.random.uniform(min_x, max_x), np.random.uniform(min_y, max_y))
        if point.intersects(polygon):
            points_list.append(point)

    return points_list

# Generate points in the clipped dissemination areas
# --------------------------------------------------

# Generate the random points
points_srs = da_clip_gdf.apply(func=random_points, 
                            args=('da_pop_2016', 'geometry', 10, 1), axis=1)

# The output is a pd.Series so convert it to a list
points_list = list(points_srs)

# Flatten the list of lists so each item in the list is a point
points_flat_list = []
for i in points_list:
    for j in i:
        points_flat_list.append(j)

# Create a GeoDataFrame of the synthetic points using the flat list as the geometry column
points_gdf = gpd.GeoDataFrame(geometry=points_flat_list, crs="EPSG:32618")

# If you made new points and want to save them,
# uncomment the line below to write them to a file
#points_gdf.to_file('data/new_points_gdf.gpkg', driver='GPKG')

# Optional: uncomment the line below to explore the points
#points_gdf.explore()

# ~15-20 mins if divisor=10

Step 2: Count the Synthetic Population Points

We now have a GeoDataFrame containing the synthetic population (points_gdf). Each point is a synthetic person that lives where dwellings are allowed within the urban land cover class. Feel free to add a new cell and use points_gdf.explore() to explore them.

We can count how many fall into each census tract, dissemination area, and neighborhood by doing the following:

1. Using the GeoPandas gpd.sjoin() method to perform a spatial join between the points and the source & target geometries
2. Assigning a value of 1 to each point
3. Grouping the features by their id/name and summing them.
4. Merging the sums of each group to the source/target geometries.

To see how exactly this works feel free to split the cells below into single expressions and then use gdf.head() on the intermediate GeoDataFrames.

For more information on these operations check out the documentation:

• gpd.sjoin()
• pd.groupby()
• pd.groupby.sum()
• pd.merge

# Count the points in each census tract
# -------------------------------------

# Spatial join of points_gdf to ct_gdf
ct_points_gdf = gpd.sjoin(points_gdf, ct_gdf, how='inner', predicate='intersects')

# Count the points that fall in each census tract
ct_points_gdf['ct_synth_pop'] = 1
ct_points_sums_gdf = ct_points_gdf.groupby(['ctuid']).sum()

# Merge the counts with the census tracts
ct_synth_gdf = ct_gdf.merge(ct_points_sums_gdf[['ct_synth_pop']], on='ctuid')

# Print the total number of points and the first 5 rows
print('Total points', ct_synth_gdf['ct_synth_pop'].sum())
ct_synth_gdf.head(5)

# Count the points in each dissemination area
# -------------------------------------------

# Spatial join of points_gdf to da_gdf
da_points_gdf = gpd.sjoin(points_gdf, da_gdf, how='inner', predicate='intersects')

# Count the points that fall in each dissemination areas
da_points_gdf['da_synth_pop'] = 1
da_points_sums_gdf = da_points_gdf.groupby(['dauid']).sum()

# Merge the counts with the census tracts
da_synth_gdf = da_gdf.merge(da_points_sums_gdf[['da_synth_pop']], on='dauid')

# Print the total number of points and the first 5 rows
print('Total points', da_synth_gdf['da_synth_pop'].sum())
da_synth_gdf.head(5)

# Count the points in each neighborhood
# -------------------------------------

# Spatial join of synthetic points to neighborhoods
nbhd_points_gdf = gpd.sjoin(points_gdf, nbhd_gdf, how='inner', predicate='intersects')

# Count the points that fall in each neighborhood
nbhd_points_gdf['nbhd_synth_pop'] = 1
nbhd_points_sums_gdf = nbhd_points_gdf.groupby(['nbhd_name']).sum()

# Merge the counts with the neighborhoods
nbhd_synth_gdf = nbhd_gdf.merge(nbhd_points_sums_gdf[['nbhd_synth_pop']], on='nbhd_name')

# Print the total number of points and the first 5 rows
print('Total points', nbhd_synth_gdf['nbhd_synth_pop'].sum())
nbhd_synth_gdf.head(5)

Step 3: Areal Interpolation of the Synthetic Population Data

Area Weighted Interpolation of Census Tracts and Dissemination Areas

The synthetic census tract and dissemination areas population data can now be used as the source for area weighted and dasymetric interpolations. We will repeat all of the steps that we took in Part 1 but this time with synthetic data.

Because these cells are are essentially copies of the cells from Part 1 there won't be any commentary until the very end. If you're unsure of what is happening in any of these cells just refer to its twin above.

# Area weighted interpolation: synthetic census tracts to neighborhoods
# ---------------------------------------------------------------------

ct_area_interp_gdf = tobler.area_weighted.area_interpolate(source_df=ct_synth_gdf, 
                                                        target_df=nbhd_synth_gdf,
                                                        extensive_variables=['ct_synth_pop'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
ct_area_interp_gdf['ct_synth_pop'] = ct_area_interp_gdf['ct_synth_pop'].round(decimals=0).astype(int)

# Rename the results column for clarity later
ct_area_interp_gdf = ct_area_interp_gdf.rename(columns={'ct_synth_pop':'ct_area_interp_est'})

# Area weighted interpolation: synthetic dissemination areas to neighborhoods
# ---------------------------------------------------------------------------

da_area_interp_gdf = tobler.area_weighted.area_interpolate(source_df=da_synth_gdf, 
                                                        target_df=nbhd_synth_gdf,
                                                        extensive_variables=['da_synth_pop'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
da_area_interp_gdf['da_synth_pop'] = da_area_interp_gdf['da_synth_pop'].round(decimals=0).astype(int)

# Rename the results column for clarity later
da_area_interp_gdf = da_area_interp_gdf.rename(columns={'da_synth_pop':'da_area_interp_est'})

Dasymetric Interpolation of Census Tracts and Dissemination Areas

# Dasymetric interpolation: synthetic census tracts + urban landover to neighborhoods
#------------------------------------------------------------------------------------

# Perform dasymetric interpolation
ct_dasy_interp_gdf = tobler.dasymetric.masked_area_interpolate(source_df=ct_synth_gdf, 
                                                            target_df=nbhd_synth_gdf,
                                                            raster='data/ottawa_landcover.tif',
                                                            codes=[17],
                                                            extensive_variables=['ct_synth_pop'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
ct_dasy_interp_gdf['ct_synth_pop'] = ct_dasy_interp_gdf['ct_synth_pop'].round(decimals=0).astype(int)

# Rename the results column for clarity later
ct_dasy_interp_gdf = ct_dasy_interp_gdf.rename(columns={'ct_synth_pop':'ct_dasy_interp_est'})

# ~30 s ; ignore warnings

# Dasymetric interpolation: synthetic dissemination areas + urban landover to neighborhoods
#------------------------------------------------------------------------------------------

# Perform dasymetric interpolation
da_dasy_interp_gdf = tobler.dasymetric.masked_area_interpolate(source_df=da_synth_gdf, 
                                                            target_df=nbhd_synth_gdf,
                                                            raster='data/ottawa_landcover.tif',
                                                            codes=[17],
                                                            extensive_variables=['da_synth_pop'])

# Round the interpolation results to the nearest integer and change the type to integer
# (Population counts must be integers)
da_dasy_interp_gdf['da_synth_pop'] = da_dasy_interp_gdf['da_synth_pop'].round(decimals=0).astype(int)

# Rename the results column for clarity later
da_dasy_interp_gdf = da_dasy_interp_gdf.rename(columns={'da_synth_pop':'da_dasy_interp_est'})

# ~1.5 mins ; ignore warnings

Step 4: Assess the Interpolation Results

# Merge the results for comparison
#---------------------------------

# Create a list of the GeoDataFrames (drop the redundant geometry)
dfs = [nbhd_synth_gdf,
        ct_area_interp_gdf.drop(columns='geometry'),
        ct_dasy_interp_gdf.drop(columns='geometry'),
        da_area_interp_gdf.drop(columns='geometry'),
        da_dasy_interp_gdf.drop(columns='geometry'),]

# Concatenate the GeoDataFrames
interp_results_gdf = pd.concat(dfs, axis=1)

# View a sample of the interpolation results GeoDataFrame (without the geometry column)
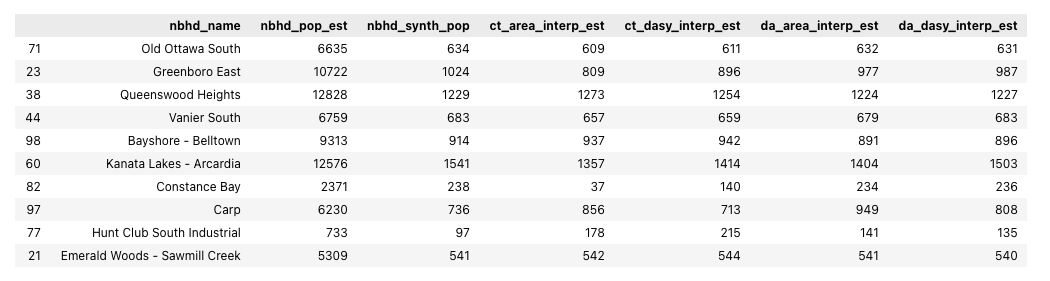
interp_results_gdf.sample(10).drop(columns='geometry')

# Evaluate Results
# ----------------

# Assign the interpolation results columns to their own variables for clarity
ct_area_est = interp_results_gdf['ct_area_interp_est'] # Source: census tracts | method: area weighted
ct_dasy_est = interp_results_gdf['ct_dasy_interp_est'] # Source: census tracts  method: dasymetric
da_area_est = interp_results_gdf['da_area_interp_est'] # Source: dissemination areas | method: area weighted
da_dasy_est = interp_results_gdf['da_dasy_interp_est'] # Source: dissemination areas | method: dasymetric
expected = interp_results_gdf['nbhd_synth_pop']        # Source: neighborhoods

# Percent Error - create new columns in interp_results_gdf
interp_results_gdf['ct_area_interp_%_error'] = round(percent_error(ct_area_est, expected), 1)
interp_results_gdf['ct_dasy_interp_%_error'] = round(percent_error(ct_dasy_est, expected), 1)
interp_results_gdf['da_area_interp_%_error'] = round(percent_error(da_area_est, expected), 1)
interp_results_gdf['da_dasy_interp_%_error'] = round(percent_error(da_dasy_est, expected), 1)

# Other statistics - create DataFrame of statistics
interp_stats_df = pd.DataFrame(data={'Interpolation Method': ['Area Weighted','Area Weighted',
                                                        'Dasymetric', 'Dasymetric'],
                                'Source Geographies': ['Census Tracts', 'Dissemination Areas',
                                                       'Census Tracts', 'Dissemination Areas'],
                                'RMSE': [rmse(ct_area_est, expected),
                                        rmse(da_area_est, expected),
                                        rmse(ct_dasy_est, expected),
                                        rmse(da_dasy_est, expected)],
                                'NRMSE': [nrmse(ct_area_est, expected),
                                        nrmse(da_area_est, expected),
                                        nrmse(ct_dasy_est, expected),
                                        nrmse(da_dasy_est, expected)],            
                                'MBE': [mbe(ct_area_est, expected),
                                        mbe(da_area_est, expected),
                                        mbe(ct_dasy_est, expected),
                                        mbe(da_dasy_est, expected)],
                                'MAE': [mae(ct_area_est, expected),
                                        mae(da_area_est, expected),
                                        mae(ct_dasy_est, expected),
                                        mae(da_dasy_est, expected)],
                                'r': [r_value(ct_area_est, expected),
                                        r_value(da_area_est, expected),
                                        r_value(ct_dasy_est, expected),
                                        r_value(da_dasy_est, expected)],
                                'r2': [r_value(ct_area_est, expected)**2,
                                        r_value(da_area_est, expected)**2,
                                        r_value(ct_dasy_est, expected)**2,
                                        r_value(da_dasy_est, expected)**2]}).round(decimals=2)

interp_stats_df

# Plot the Percent Error of Both Methods using a Plotly Facet Map
# ---------------------------------------------------------------

# Convert interp_results_gdf from GeoDataFrame to GeoJson
geojson = interp_results_gdf.to_crs(epsg='4326').to_json()
geojson = json.loads(geojson)

# Reformat the interp_results_gdf for the plot
df = pd.DataFrame(interp_results_gdf.drop(columns='geometry'))

df = df.rename(columns={'ct_area_interp_%_error':'Source: Census Tracts <br> Method: Area Weighted',
                'ct_dasy_interp_%_error':'Source: Census Tracts <br> Method: Dasymetric',
                'da_area_interp_%_error':'Source: Dissemination Areas <br> Method: Area Weighted',
                'da_dasy_interp_%_error':'Source: Dissemination Areas <br> Method: Dasymetric'})

df = df.melt(id_vars='nbhd_name',
            value_vars=['Source: Census Tracts <br> Method: Area Weighted',
                        'Source: Census Tracts <br> Method: Dasymetric',
                        'Source: Dissemination Areas <br> Method: Area Weighted',
                        'Source: Dissemination Areas <br> Method: Dasymetric'],
            var_name='method', 
            value_name='Error (%)')

# Create the Plotly Express choropleth figure
fig = px.choropleth(data_frame=df,
                    title="Areal Interpolation of Synthetic Population Data to Ottawa, ON Neighborhoods",
                    locations='nbhd_name',
                    geojson=geojson,
                    featureidkey='properties.nbhd_name',
                    color='Error (%)',
                    facet_col='method',
                    facet_col_wrap=2,
                    hover_name='nbhd_name',
                    range_color=[0,100],
                    color_continuous_scale='Inferno',
                    projection='mercator',
                    fitbounds="locations",
                    height=800, width=800)
         
fig.for_each_annotation(lambda a: a.update(text=a.text.split('=')[-1]))
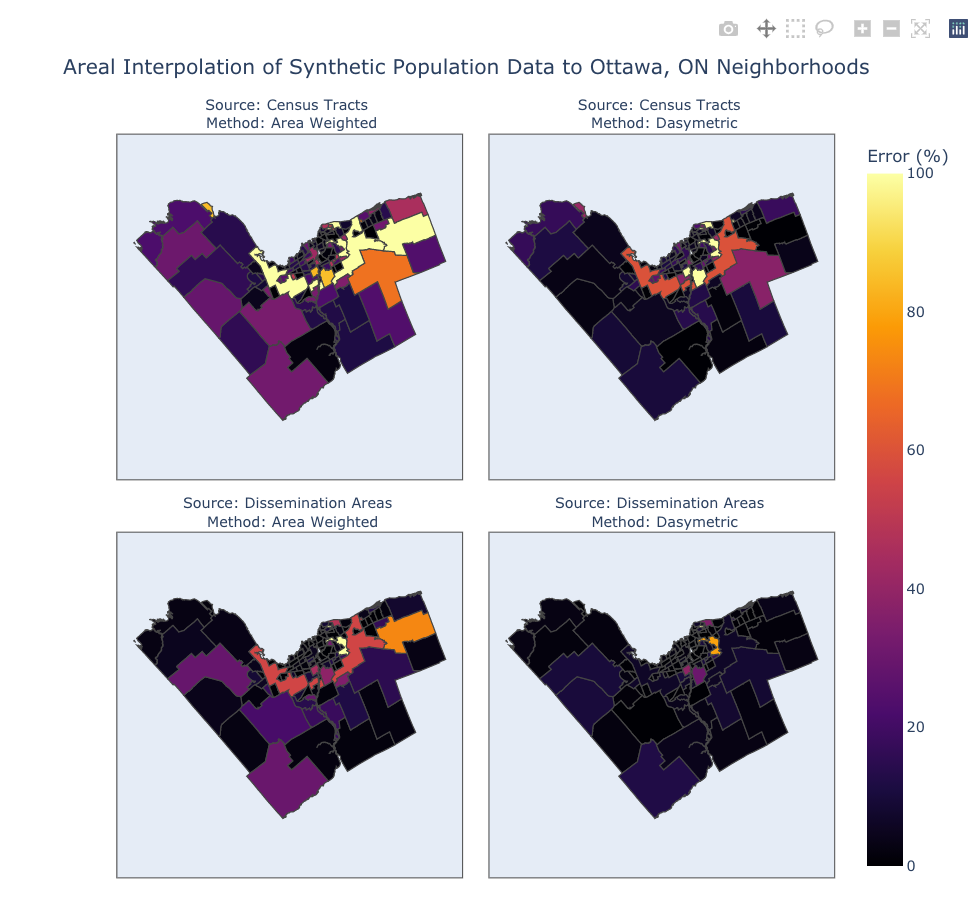
fig.show()

# Create 1:1 Facet Plots using Plotly
# -----------------------------------

# Convert the interpolation results to a DataFrame
df = pd.DataFrame(data=interp_results_gdf.drop(columns='geometry'))

# Rename the results columns as they will become the facet plot labels
df = df.rename(columns={'ct_area_interp_est':'Source: Census Tracts <br> Method: Area Weighted',
                'ct_dasy_interp_est':'Source: Census Tracts <br> Method: Dasymetric',
                'da_area_interp_est':'Source: Dissemination Areas <br> Method: Area Weighted',
                'da_dasy_interp_est':'Source: Dissemination Areas <br> Method: Dasymetric'})

# Combine all the results columns into one column
df = df.melt(id_vars=['nbhd_name', 'nbhd_synth_pop'],
            value_vars=['Source: Census Tracts <br> Method: Area Weighted',
                        'Source: Census Tracts <br> Method: Dasymetric',
                        'Source: Dissemination Areas <br> Method: Area Weighted',
                        'Source: Dissemination Areas <br> Method: Dasymetric'],
            var_name='method', 
            value_name='interp_pop_est')

# Add a percent error column
estimated = df['interp_pop_est']
expected = df['nbhd_synth_pop']
df['%_error'] = round(percent_error(estimated, expected), 1)

# Create the Plotly Express Scatter figure
fig = px.scatter(data_frame=df,
                title="Areal Interpolation of Synthetic Population Data to Ottawa, ON Neighborhoods",
                x='nbhd_synth_pop',
                y='interp_pop_est',
                height=800, width=800,
                color='%_error',
                facet_col='method',
                facet_col_wrap=2,
                hover_name='nbhd_name',
                labels={'interp_pop_est': 'Interpolated Population',
                        'nbhd_synth_pop': ' Estimated Population'},
                color_continuous_scale='Inferno',
                range_color=[0,100])

# Create the 1:1 line
line_max = max([max(df['interp_pop_est']), max(df['nbhd_synth_pop'])])
line_min = min([min(df['interp_pop_est']), min(df['nbhd_synth_pop'])])

fig.update_layout(shapes=[
        dict(type='line', xref='x', yref='y',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1),
        dict(type='line', xref='x2', yref='y2',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1),
        dict(type='line', xref='x3', yref='y3',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1),
        dict(type='line', xref='x4', yref='y4',
            x0=line_min, y0=line_min, x1=line_max, y1=line_max, line_width=1)])

fig.for_each_annotation(lambda a: a.update(text=a.text.split('=')[-1]))

fig.show()

Conclusion

Looking at the statistical and visual representations of the synthetic results we can see a familiar pattern emerge. The error and correlation values show that when choosing between census tracts and dissemination areas the latter is the better choice. Also, when comparing between the two different approaches to interpolation, the dasymetric method is superior that the simple area weighted method. Bear in mind, the model in Part 2 is quite over-fit as we used the same land cover raster for the dasymetric interpolation and to create the bounds within which the synthetic points were generated - in reality there would quite a bit more variation. Despite this issue, I believe we can still conclude that using the finest spatial resolution of source data, whether through the choice geometries, or through the contribution of secondary information such as land cover, will give the best results when performing areal interpolation.

Where do we go from here? Well, other areal interpolation methods exits, for example Tobler offers functions for model-based and pycnophylactic interpolation, so future exercises could examine those methods and how they compare. It's likely that by using higher quality secondary data and taking more spatial considerations into account, the results can be improved even further.

I hope that this tutorial was interesting and has helped to expand your familiarity with areal interpolation, Tobler, Pandas, GeoPandas, and Plotly. If you want to propose any changes, feel free to submit a pull request to this tutorial's github repository or find me at my Twitter account.